Bit Masking in Java
1. Introduction Bit masking is visualizing a number or other data in binary representation. Some bits are set and others
examples.javacodegeeks.com
1. 소개
비트 마스킹은 숫자 또는 그 외의 데이터들을 이진 표현으로 시각화하는 것입니다.설정은 true 또는 1을 의미하고 설정 해제는 false 또는 0을 의미하는 이 방식은 일부 비트를 설정되고 그 외 나머지 비트는 설정하지 않습니다.
이런 방식은 하나의 숫자 값으로 여러 값을 저장 하도록 만들어 줍니다.
우리는 이 숫자를 전체로 생각하는 대신 각각 비트를 별도의 값으로 대응해서 생각해야 합니다.
2. 비트마스킹 (Bitmasking)
비트마스킹은 특정 비트만 통과시키고 나머지 비트는 마스킹 처리를 하는 작업입니다.
예를 들어 설명해보면, 이 개념은 더 잘 이해할 수 있습니다.
우리가 숫자 10이 있으면 이 십진수 (10)10의 이진법 표현은 (1010)2입니다.
이제 우리가 이 숫자의 세 번째 비트가 설정되어 있는지 여부를 찾고 싶다고 가정해 보겠습니다.
이 문제를 해결하기 위해 비트 AND 연산자를 사용 할 것입니다. 그리고, 여기서 우리는 세 번째 비트가 설정되어 있는지 여부를 찾아야 하는 경우이므로 다른 비트들에는 관심이 없습니다.
따라서 최 하위 비트(수)에서 최 상위 비트(수) - 오른쪽에서 왼쪽 - 로 이동하면서 우리는 첫 번째(0), 두 번째(1) 및 네 번째(1) 비트에 관심이 없으므로 이들을 마스킹할 것입니다.
마스킹이란 것은 0으로 비트 AND 연산을 적용한다는 것을 의미로 받아 들이면 될 것입니다.
비트 'x'(0/1)가 있고 0과 AND하면 항상 0이 될 것이며,
비트 'x'(0/1)가 있고 1과 AND하면 항상 1이 될 것입니다.
– 예를 들어:
x = 0 이면 0 & 1 = 0(x)이고,
x = 1이면 1 & 1 = 1(x)
입니다.
통과시키려는 비트는 1과 AND 비트 연산를 할 것입니다. 그래서 위의 예 0100과 1010를 AND 비트연산을 할 것입니다.
참고: 오직 왼쪽에서 세 번째 비트만 1이고 나머지는 0입니다.
비트연산 AND를 수행할 때 0이 아닌 숫자를 얻으면 해당 특정 비트가 설정되었다는 것이며 그렇지 않으면 설정되지 않았다는 것을 의미 합니다.
우리 예에서는 세 번째 비트가 설정되지 않았음을 의미하는 0(1010 & 0100 = 0000)을 얻을 것입니다.
3. 비트 마스크 만들기
이 섹션에서 두리는 이 비트 마스크를 만드는 방법을 살펴볼 것입니다.
k번째 비트가 설정되어 있는지 확인하려면 1을 k-1번(1 << (k-1))으로 왼쪽 시프트 하는 것일 것입니다.
따라서 첫 번째 비트의 마스크를 찾으려면 1을 왼쪽 시프트 1한다면 1 – 1 = 0이 될 것입니다. 따라서 값은 0001이 됩니다.
예를 들어 ((10)10) (1010)2 & (0001)2 = (0000)2이므로 첫 번째 비트가 설정되지 않았음을 알 수 있습니다.
그럼, second(1) 비트를 확인해봅시다.
마스크를 찾기 위해 왼쪽 시프트 1을 1(2 – 1) 비트로 할 것이므로 0010 값을 얻을 것입니다.
이제 1010 & 0010을 수행하면 0이 아닌 (0010)2를 얻으므로 두 번째 비트가 설정되어 있다는 것을 우리는 알 수가 있습니다.
public static void main(String[] args)
{
//1을 왼쪽으로 1 시프트
String shift_1 = Integer.toBinaryString(1 << (1-1));
System.out.println(shift_1);
//1을 왼쪽으로 2 시프트
String shift_2 = Integer.toBinaryString(1 << (2-1));
System.out.println(shift_2);
//1을 왼쪽으로 5 시프트
String shift_5 = Integer.toBinaryString(1 << (5-1));
System.out.println(shift_5);
String sval = "10001";
//int val = Integer.parseInt("10001");
//첫 번째 비트 설정여부
String first_setbit = Integer.toBinaryString(Integer.parseInt(sval, 2) & Integer.parseInt(shift_1, 2));
System.out.println(first_setbit);
int num1 = Integer.parseInt(first_setbit, 2) >> (1-1) & 0xFF;
System.out.println(num1);
//두 번째 비트 설정여부
String second_setbit = Integer.toBinaryString(Integer.parseInt(sval, 2) & Integer.parseInt(shift_2, 2));
System.out.println(second_setbit);
num1 = Integer.parseInt(second_setbit, 2) >> (2-1) & 0xFF;
System.out.println(num1);
//5 번째 비트 설정여부
String fifth_setbit = Integer.toBinaryString(Integer.parseInt(sval, 2) & Integer.parseInt(shift_5, 2));
System.out.println(fifth_setbit);
num1 = Integer.parseInt(fifth_setbit, 2) >> (5-1) & 0xFF;
System.out.println(num1);
}1
10
10000
1
1
0
0
10000
14. 모든 조합 찾아보기
이 섹션에서는 비트 마스킹을 사용하여 몇 가지 복잡한 문제에 대한 솔루션을 찾는 방법을 살펴 볼 것입니다.
3개의 요소 S -> {X, Y, Z}를 갖는 집합 S가 주어졌다고 가정해 보겠습니다.
이제 우리는 주어진 집합 S의 모든 가능한 하위 집합을 찾아야 한다고 합시다.
4.1 재귀
이 문제를 해결하기 위해 집합의 각 요소에서 가능한 하위집합의 가능성에는 무엇인지 확인 해야 합니다.
이 경우의 경우의 수는 두 가지뿐입니다. 해당 요소를 포함하거나 제외 할 수 있는 것입니다.
따라서 X에는 두 가지 가능성이 있습니다. – I(Included), and E(Excluded), Y와 Z 도 X의 경우와 같이 이 두개의 경우의 수를 가질 것입니다.
그래서 각 요소는 두가지 선택을 가집니다 - 전체 선택 개수는 2 * 2 * 2 = 23 = 8 이 될 것입니다.
우리가 n개의 요소를 가지고 있다면 여기에서 경우의 수는 2n이 됩니다.

위의 다이어그램은 재귀 트리를 나타냅니다.
X에 있을 때 X를 포함하거나 제외하는 것이 두 가지 옵션입니다. 녹색 선은 포함을 나타내고 빨간색은 제외를 나타냅니다.
만약 이 트리 다이어그램을 따라가면 맨 아래 줄이 가능한 하위 집합의 수를 나타낸다는 것을 알 수 있을 것입니다.
n개의 요소를 포함하는 집합의 범위는 아무것도 선택 되지 않은 빈 부분 집합에서 모든 요소를 포함하는 부분 집합까지 일 것입니다.
4.2 비트 마스크
이 섹션에서는 비트 마스크를 사용하여 위의 문제를 해결하는 방법을 살펴 볼 것입니다.
우리는 제외를 나타내기 위해 0을 사용하고 포함을 나타내기 위해 1을 사용 할 것입니다.
예를 들어:
X, Y, Z 요소를 포함하는 집합이 있는 경우에 우리는 마스크 값으로 100을 선택 할 수 있습니다.
이 값을 선택 한다는 것은 X가 포함되고 Y와 Z가 제외 된다는 것을 의미 할 것입니다.
따라서 {X,Y,Z} -> 100 = {A}를 의미합니다.
그럼 우리가 모든 요소를 제외하려 한다면 마스크가 000 이어야 하고 모든 요소를 포함하려 한다면 111 되어야 합니다.
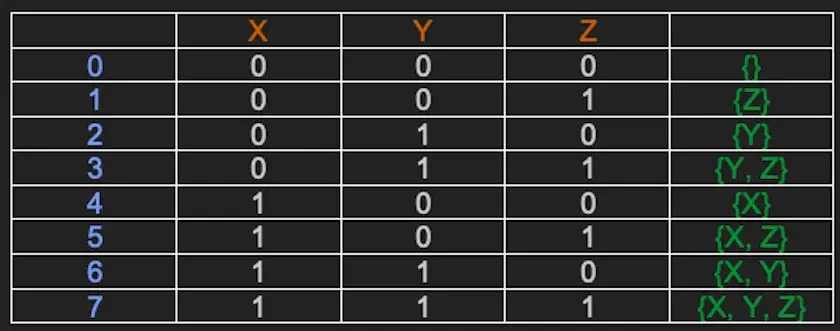
위의 그림에서 첫 번째 요소가 0인 두 번째 행은 요소가 포함되지 않은 조합을 나타내고 마지막 행은 모든 요소가 포함된 조합을 나타냅니다. 위 그림에서 모두 0인 가진 두 번째 행은 아무것도 없는 요소를 포함한 조합을 나타내며 첫번째 요소이며, 마지막 행은 모든 요소들이 포함된 조합을 나타내고 있습니다.
범위는 0에서 2n -1이며, 이 경우에는 23 – 1 = 7입니다.
따라서 당신이 주어진 요소(예: n)에 대한 비트마스크를 생성한다면, 0에서 2n-1까지 루프 실행을 해야 한다는 것입니다.
굳이 위의 내용을 어거지로 때려 맞춘다고 코드를 작성 해 보았습니다.
public static void test2()
{
//1을 왼쪽으로 1 시프트
String shift_1 = Integer.toBinaryString(1 << (1-1));
//1을 왼쪽으로 2 시프트
String shift_2 = Integer.toBinaryString(1 << (2-1));
//1을 왼쪽으로 2 시프트
String shift_3 = Integer.toBinaryString(1 << (3-1));
int possibility = 3;
int total = (int)Math.pow(2, possibility);
System.out.printf("val X Y Z\n");
for(int i = 0; i < total; i++)
{
String val = Integer.toBinaryString(i);
String first_setbit = Integer.toBinaryString(Integer.parseInt(val, 2) & Integer.parseInt(shift_1, 2));
String second_setbit = Integer.toBinaryString(Integer.parseInt(val, 2) & Integer.parseInt(shift_2, 2));
String third_setbit = Integer.toBinaryString(Integer.parseInt(val, 2) & Integer.parseInt(shift_3, 2));
int num1 = Integer.parseInt(first_setbit, 2) >> (1-1) & 0xFF;
int num2 = Integer.parseInt(second_setbit, 2) >> (2-1) & 0xFF;
int num3 = Integer.parseInt(third_setbit, 2) >> (3-1) & 0xFF;
System.out.printf("%s %d %d %d\n", i, num1, num2, num3);
}
}결과
10
100
val X Y Z
0 0 0 0
1 1 0 0
2 0 1 0
3 1 1 0
4 0 0 1
5 1 0 1
6 0 1 1
7 1 1 15. 결론
이번 글에서는 비트 마스킹에 대해 알아보았습니다.
우리는 비트 마스킹의 의미와 이러한 마스크를 만드는 방법을 살펴보았습니다.
마지막으로 우리는 두 가지 방법을 사용하여 문제를 해결하는 방법을 살펴보았습니다 -
첫 번째는 재귀를 사용하는 것이고
두 번째 방법은 비트 마스크를 사용하는 것입니다.
'프로그래밍' 카테고리의 다른 글
| Python에서 문자열을 비교하는 방법: 동일성과 동등성 (0) | 2022.11.28 |
|---|---|
| Where, Group by, Holding 및 Order by 절 (0) | 2022.11.27 |
| final 키워드가 자바 가비지콜렉션을 향상 시킬까요? (0) | 2022.11.25 |
| [C#]제공자가 oracle 클라이언트 버전과 호환되지 않습니다 (0) | 2022.11.24 |
| Python 101: Equality(동일성) vs Identity(동등성) (0) | 2022.11.23 |

