1. 소개
이번 글에서는 Sorting Algorithm의 일종인 Bucket Sort Algorithm에 대해 구체적으로 살펴보도록 하겠습니다. 일반적으로 알고리즘은 문제를 해결하거나 특정 결과를 달성하기 위해 순차적으로 실행할 수 있는 일련의 명령으로 생각할 수 있습니다. 알고리즘은 일반적으로 수학 또는 컴퓨팅 직업에서 다양한 종류의 문제를 해결하는 데 사용됩니다.
컴퓨팅에서 알고리즘은 문제를 해결하는 데 있어 유사성과 기능에 따라 여러 유형으로 분류할 수 있습니다.
다음은 컴퓨터 과학의 알고리즘 유형의 예입니다:
- Searching Algorithms
- Sorting Algorithms
- Hashing Algorithms
- Recursive Algorithms
- Dynamic Programming Algorithms
- Brute Force Algorithms
- Randomized Algorithms and
- Greedy Algorithms.
여기에서는 정렬 알고리즘 유형 중 하나인 버킷 정렬 알고리즘에 중점을 둡니다.
2. 이 버킷 정렬 예제에 사용할 기술
운영 체제: Ubuntu 20.04 또는 Windows 10.
IDE: (Ubuntu의 IntelliJ IDEA Community Edition 2022.2) 또는 (Windows 10의 IntelliJ IDEA2021.3.3 Community Edition).
(Ubuntu의 Java OpenJDK 버전 11.0.16) 및 (Windows의 Java JDK 1.8.0_341).
3. 버킷 정렬 알고리즘
버킷 정렬 알고리즘은 정렬되지 않은 요소 배열을 버킷이라는 더 작은 요소 그룹 또는 목록으로 나누는 방식으로 작동합니다. 그런 다음 이러한 각 버킷을 개별적으로 정렬한 다음 정렬된 모든 버킷을 하나의 정렬된 배열로 병합합니다.
버킷 정렬 알고리즘은 기본 정렬되지 않은 배열을 더 작은 버킷(배열 또는 목록)으로 나누고 개별 버킷을 정렬하고 정렬된 버킷을 완전히 정렬된 배열로 병합하는 데 사용되는 메커니즘인 Scatter Gather(분산 수집) 접근 방식을 사용합니다.
4. Scatter-Gather(분산-수집) 접근
버킷 정렬 알고리즘은 다음 단계를 구현합니다.
- 빈 버킷 목록(또는 적절한 데이터 구조) List<ArrayList<>>를 만듭니다.
- N + 1의 크기로 초기화합니다. 여기서 N은 배열의 요소 수입니다.
- unsortedArray[ ]에서 최대값 M을 찾습니다.
- 정렬되지 않은 배열 unsortedArray[ ]를 탐색할 때 다음과 같이 버킷 인덱스를 계산하여 unsortedArray[ i ]의 각 배열 요소를 버킷 목록에 삽입합니다. bucketIndex = [floor(N * array[ i ] / M)]
- 배열의 요소가 float 유형인 경우 다음 공식을 사용하여 버킷 인덱스를 계산합니다. [N * unsortedArray[ i ]].
- 적절한 정렬 알고리즘을 사용하여 각 버킷을 정렬하거나 버킷 정렬을 사용하여 재귀적으로 정렬합니다.
- 정렬된 버킷을 정렬된 배열로 병합합니다.
이것은 다음과 같은 시각적 예를 통해 설명됩니다.

버킷 정렬 알고리즘의 이 데모에서는 버킷 목록의 데이터 구조로 ArrayList의 목록을 사용합니다.
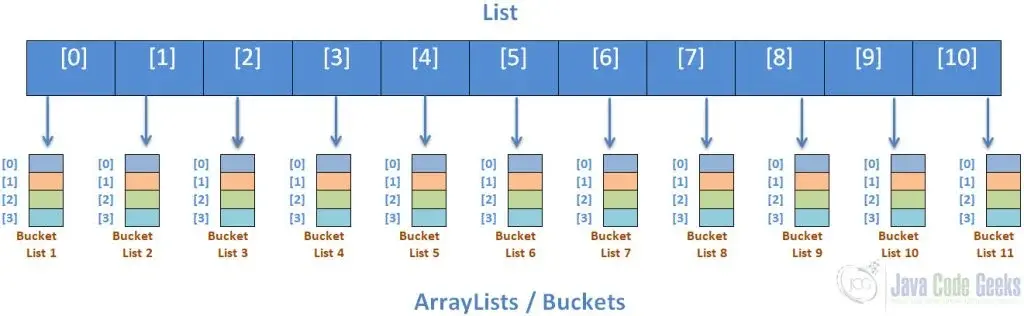
The Scatter Approach(분산 접근법)
여기에서 정렬되지 않은 배열 unsortedArray[ ]의 요소는 별도의 버킷으로 분할되고 배치될 각 버킷의 인덱스는 다음과 같이 계산됩니다.

그런 다음 요소는 다음과 같이 분할됩니다.
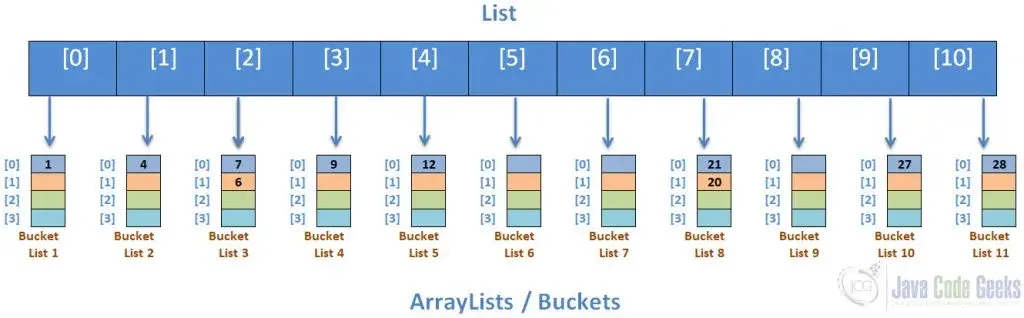
그런 다음 버킷은 정렬 알고리즘을 사용하여 정렬됩니다.
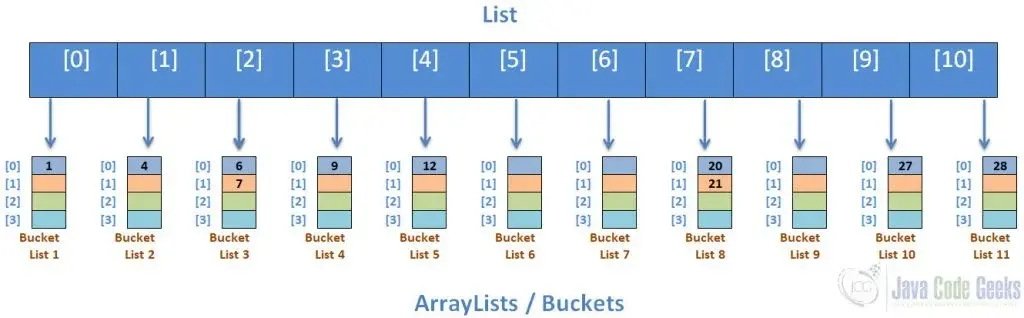
The Gather Approach(수집 접근 방식)
수집 접근 방식에는 다음과 같이 정렬된 버킷을 정렬된 배열로 병합하는 작업이 포함됩니다.
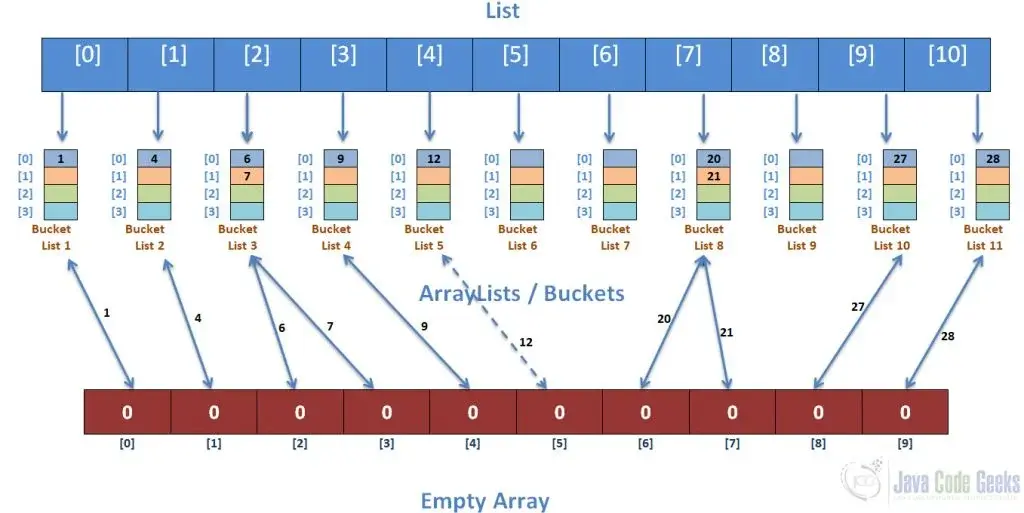
마지막으로 정렬된 ArrayList 값이 아래와 같이 배열에 복사됩니다.

5. 버킷 정렬 구현
다음은 버킷 정렬 알고리즘의 Java 구현입니다.
package com.javacodegeeks.bucketsort;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BucketSort {
//A getMaxValue function to determine the maximum value in an array.
public static int getMaxValue(int[] m){
int maxValue = 0;
for(int i = 0; i maxValue){
maxValue = m[i];
}
}
return maxValue;
}
//A printOutPut method to display the contents of the sorted array.
public static void printOutput(int[] sortedArray){
System.out.println(" The sorted array is as follows:");
for(int i = 0; i < sortedArray.length; i++){
System.out.print(sortedArray[i] + " ");
}
}
//This implementation of the Bucket Sort Algorithm uses a List of ArrayLists as the bucket data structure.
public static int[] bucketSortAlgorithm(int[] unsortedArray){
int n = unsortedArray.length;
int maxElement = getMaxValue(unsortedArray);
int bucketListSize = n + 1;
//Create the bucket list and initialize it to the size of the unsortedArray's length + 1.
List<ArrayList> buckets = new ArrayList(bucketListSize);
//Create empty buckets
for(int i = 0; i < bucketListSize; i++) {
buckets.add(new ArrayList());
}
/*Traverse the unsortedArray and arrange the elements into buckets.
This is the Scatter part in the Scatter Gather Approach.*/
int bucketIndex = 0;
for(int i = 0; i < n; i++){
bucketIndex = (int)(Math.floor((unsortedArray[i] * n)/maxElement));
buckets.get(bucketIndex).add(unsortedArray[i]);
System.out.println("The added elements are: ");
System.out.println(buckets);
}
/*Sort each bucket using an appropriate sorting algorithm or recursively use
the Bucket Sort Algorithm*/
for(int i = 0; i < bucketListSize; i++){
Collections.sort(buckets.get(i));
System.out.println("The sorted buckets are as follows:" + buckets);
}
/*Merge the sorted buckets into a single sorted array
This is known as the Gather part in the Scatter Gather Approach*/
int arrayIndex = 0;
List sortedArrayList = new ArrayList();
for(int i = 0; i < bucketListSize; i++){
int bucketSize = buckets.get(i).size();
for (int j = 0; j < bucketSize; j++) {
List intValue = buckets.get(j);
sortedArrayList.add(buckets.get(i).get(j));
}
}
//Copy the contents of the sorted List into an empty array.
int[] sorted_arr = sortedArrayList.stream().mapToInt(Integer::intValue).toArray();
return sorted_arr;
}
public static void main(String[] args) {
int[] array = {12, 27, 4, 7, 28, 9, 21, 1, 20, 6};
/*The following arrays can be uncommented and tested to see how the Algorithm works with different values*/
//int[] array = {67, 23, 2, 80, 44, 90, 33, 56, 73, 7, 25, 14, 48, 69, 84, 78, 36, 52, 18, 62};
//int[] array = {94, 87, 3, 77, 16, 35, 67, 5};
//Display of the unsorted Array before sorting.
System.out.println("The unsorted array is as follows:" );
for(int i = 0; i < array.length; i++){
System.out.print(array[i] + " ");
}
//A BucketSort object is created.
BucketSort b = new BucketSort();
//The BucketSort object is used to make a call to the bucketSort Algorithm and the output is displayed.
printOutput(b.bucketSortAlgorithm(array));
}
}결과 값:
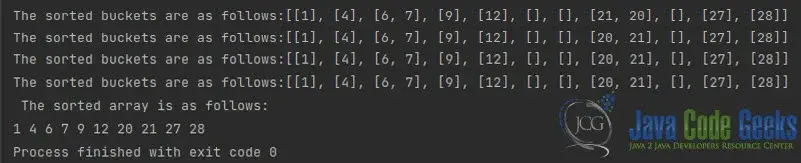
또는 아래에서 이 예제의 소스 코드를 다운로드하여 원하는 IDE에서 실행할 수 있습니다.
6. 알고리즘의 복잡도
알고리즘을 실행하는 데 필요한 시간, 저장소 또는 기타 리소스의 양을 알고리즘의 계산 복잡도이라고 합니다.
다음 두 가지 방법 중 하나로 결정할 수 있습니다.
- 시간 복잡도 또는
- 공간 복잡도가 그것입니다.
알고리즘의 시간 복잡도는 입력 크기가 증가함에 따라 처리 속도 측면에서 알고리즘의 성능을 결정합니다. 이를 기본적으로 알고리즘의 실행 시간이라고 하며 매우 큰 데이터 세트와 함께 사용할 때 알고리즘이 수행하는 작업 수를 계산하여 추정합니다.
알고리즘의 공간 복잡도는 명령 또는 단계를 실행하는 동안 알고리즘이 사용하는 메모리의 양을 고려합니다.
일반적으로 알고리즘은 작동하는 입력 또는 데이터 세트에 따라 다른 속도로 수행됩니다. 작은 입력에 대한 알고리즘의 성능은 중요하지 않을 수 있지만 입력 크기가 커질수록 성능이 테스트됩니다.
버킷 정렬 알고리즘이 최상의 성능을 발휘하려면 생성된 버킷의 수가 배열 또는 사용된 데이터 구조의 요소 수와 같아야 합니다. 이렇게 하면 요소가 여러 버킷에 분산되고 시간 복잡도가 O(N)이 됩니다. 이것은 Best Case Time Complexity로 알려져 있습니다.
알고리즘에 대한 버킷 수를 잘못 선택하면(예: 버킷 하나만 사용하도록 선택하면 알고리즘의 성능에 큰 영향을 미칩니다.) 이러한 경우는 Worst Case 시나리오로 간주되며 시간 복잡도는 O(N2)가 됩니다.
알고리즘의 전체 성능은 각 버킷을 개별적으로 정렬하는 데 사용되는 알고리즘에 의해 결정됩니다. 결과적으로 최악의 시나리오는 O(N2)에서 O(NLogN)까지입니다.
7. 결론
airfocus.com에 따른 버킷 정렬 알고리즘의 실제 적용은 다음과 같습니다:
- 데이터 세트의 정렬 프로세스를 가속화하고
- 소요 시간을 기준으로 우선 순위 목록을 구성하고 할당합니다.
8. 소스 코드 다운로드
여기까지 BucketSort 알고리즘의 예제 였습니다.
'프로그래밍' 카테고리의 다른 글
| [C#]제공자가 oracle 클라이언트 버전과 호환되지 않습니다 (0) | 2022.11.24 |
|---|---|
| Python 101: Equality(동일성) vs Identity(동등성) (0) | 2022.11.23 |
| 쿠버네티스-Pod 관련 실행 연습 (0) | 2022.11.20 |
| Kubernetes? 쿠버네티스? (0) | 2022.11.19 |
| Python에서 순홤문을 작성하는 방법: While 및 For (1) | 2022.11.18 |