https://www.javatpoint.com/data-structure-asymptotic-analysis
DS Asymptotic Analysis - javatpoint
DS Asymptotic Analysis with Introduction, Asymptotic Analysis, Array, Pointer, Structure, Singly Linked List, Doubly Linked List, Circular Linked List, Binary Search, Linear Search, Sorting, Bucket Sort, Comb Sort, Shell Sort, Heap Sort, Merge Sort, Select
www.javatpoint.com
데이터 구조 라는 것은 데이터를 효율적으로 구성하는 방법이며 이에 대한 효율성은 시간 또는 공간 측면에서 측정 할 수 있습니다.
따라서 이상적인 데이터 구조는 모든 작업을 수행하는 데 가능한 최소한의 시간과 메모리 공간을 차지하는 구조입니다.
우리는 이 구조에서 공간 복잡도보다 시간 복잡도를 찾는 데 촛점을 맞추고 있으며, 시간 복잡도를 찾음으로써 어떤 데이터 구조가 알고리즘에 가장 적합한지 결정할 수 있습니다.
데이터 구조의 시간 복잡도를 비교해야 할 때 비교 해야 하는 기준은 무엇일까요?
시간 복잡도는 수행된 작업을 기반으로 비교할 수 있습니다. 간단한 예를 들어 봅시다.
우리가 100개의 요소를 가진 배열이 만들고 배열의 시작 부분에 새 요소를 삽입하려고 한다고 가정 해 봅시다. 우선 요소를 오른쪽으로 이동하고 배열 첫 부분으로 이동해서 새로운 요소를 추가해야 하는 매우 지루한 작업이 될 것입니다.
첫 부분에 요소를 추가하는 작업에 대한 데이터 구조로 linked list을 선택 했다고 가정 하겠습니다.
linked list는 두 부분, 즉 데이터와 다음 노드의 주소를 가집니다.
우리는 간단히 새로운 노드에 첫 번째 노드의 주소를 추가하면 헤드 포인터가 새로 추가된 노드를 가리킬 것입니다.
따라서 linked list의 첫부분에 데이터를 추가하는 것이 배열보다 빠르다는 결론에 도달 했습니다.
이러한 방식으로 데이터 구조를 비교하고 작업 수행에 가장 적합한 데이터 구조를 선택할 수 있습니다.
작업 수행을 위한 시간 복잡도 또는 실행 시간을 어떻게 찾을 수 있을까?
실제 실행 시간의 측정은 전혀 실용적이지 않습니다. 해당 작업을 수행하는 실행 시간은 입력 크기에 따라 다를 것입니다.
간단한 예를 통해 이 말이 맞는 지 확인해 봅시다.
우리는 5개 요소의 배열을 가지고 있으며,
이 배열의 첫 머리에 새 요소를 추가하려고 한다고 가정합니다. 새 요소를 추가하기 위해서는 배열의 각 요소를 오른쪽으로 이동시켜야하며 각 요소를 옮기는 데 1의 시간 단위를 가진다고 가정해 봅시다.
우리는 5개의 요소가지고 있으므로, 단위 5의 시간이 소요됩니다. 배열에 1000개의 요소가 있고 이동시키는 데 1000단위의 시간이 걸린다고 가정하면, 시간 복잡도는 입력 크기에 따라 달라진다는 결론이 납니다.
따라서 입력 크기가 n이면 f(n)은 시간 복잡도를 나타내는 n의 함수입니다.
f(n)을 계산하는 방법은?
좀 작은 프로그램에 대한 f(n) 값의 계산은 쉽지만 큰 프로그램에 대해서는 그렇게 쉽지 않습니다. 우리는 이 f(n) 값들을 비교 함으로써 데이터 구조들을 비교할 수 있습니다.
어떤 하나의 데이터 구조가 좀 더 작은 입력 크기에 대해서는 다른 것보다 더 좋지만 이보다 더 큰 크기에 대해서는 그렇지 않을 가능성이 있기 때문에 우리는 f(n)의 증가율을 찾아 볼 것입니다.
그럼 f(n)을 찾는 방법입니다.
간단한 예를 살펴 봅시다.
f(n) = 5n2 + 6n + 12
여기서 n은 실행된 명령의 수이며 입력 크기에 따라 다릅니다.
n=1 일 때,
5n2로 인한 실행 시간의 % = 점근적 분석 * 100 = 21.74%
6n으로 인한 실행 시간의 % = 점근적 분석 * 100 = 26.09%
12로 인한 실행 시간의 % = 점근적 분석 * 100 = 52.17%
위의 계산 값을 살펴보면 대부분의 시간이 12에 걸린다는 것을 알 수 있습니다. 하지만 우리는 f(n)의 증가율을 찾아야만 하기 때문에, 최대 시간이 12에 걸린다고 말할 수는 없습니다.
그럼, n 의 차이 값들이 f(n)의 증가율을 찾는 것이다라고 가정 해 봅시다.
f(n)의 성장률을 찾기 위한 n의 여러 값.
|
n
|
5n^2
|
6n
|
12
|
|
1
|
21.74%
|
26.09%
|
52.17%
|
|
10
|
87.41%
|
10.49%
|
2.09%
|
|
100
|
98.79%
|
1.19%
|
0.02%
|
|
1000
|
99.88%
|
0.12%
|
0.0002%
|
위의 표에서 알 수 있듯이 n 값이 증가함에 따라 6n 및 12의 실행 시간도 감소하면 5n2의 실행 시간이 증가하고 있습니다. 따라서 n 값이 클수록 제곱 항이 거의 99%의 시간을 소비하는 것으로 관찰됩니다. n2 항이 대부분의 시간에 잡아먹고 있으므로, 나머지 두 항을 제거할 수 있습니다.
그래서,
f(n) = 5n2
여기에서 결과가 실제 결과에 매우 가까운 대략적인 시간 복잡도를 얻고 있습니다.
그리고 이 대략적인 시간 복잡도 측정은 점근적 복잡도로 알려져 있습니다. 여기서는 정확한 러닝타임을 산정하는 것이 아니라 불필요한 항를 없애고 가장 시간이 많이 걸리는 항만을 고려하고 있습니다.
수학적 분석에서 알고리즘의 점근적 분석은 런타임 성능의 수학적 경계를 정의하는 방법입니다. 점근 분석을 사용하면 알고리즘의 평균의 경우, 최상의 경우 및 최악의 경우에 대한 시나리오를 쉽게 결론을 내릴 수 있습니다.
이것으로 알고리즘 내부의 모든 작업 실행 시간을 수학적으로 계산하는 데 사용됩니다.
예: 한 작업의 실행 시간은 x(n)이고 나머지 작업의 경우 f(n2)로 계산됩니다. 첫 번째 작업에서는 'n'이 증가함에 따라 실행 시간이 선형적으로 증가하고 두 번째 작업에서는 실행 시간이 기하급수적으로 증가하는 것을 뜻합니다. 마찬가지로 n이 상당히 작은 경우 두 작업의 실행 시간은 동일합니다.
Usually, the time required by an algorithm comes under three types:
일반적으로 알고리즘에서 말하는 이 시간은 다음 세 가지 유형으로 나뉩니다:
Worst case: It defines the input for which the algorithm takes a huge time.
최악의 경우: 알고리즘에 많은 시간이 걸리는 입력을 정의합니다.
Average case: It takes average time for the program execution.
평균적인 경우: 프로그램 실행에 평균적인 시간이 걸립니다.
Best case: It defines the input for which the algorithm takes the lowest time
최상의 경우: 알고리즘이 가장 시간이 적게 걸리는 입력을 정의합니다.
점근적 표기법
알고리즘의 실행 시간 복잡도를 계산하는 데 사용되는 일반적으로 사용되는 점근적 표기법은 다음과 같습니다:
- 빅오(Big oh) 표기법 (O)
- 오메가 표기법(Ω)
- 세타 표기법(θ)
빅오 표기법(O)
- Big O 표기법은 단순히 함수의 성장 순서(the order of growth)를 제공하여 알고리즘의 성능을 측정하는 점근적 표기법입니다.
- 이 표기법은 함수가 상한보다 빠르게 증가하지 않도록 하는 함수의 상한을 제공합니다. 따라서 함수에 최소 상한을 부여하여 함수가 이 상한보다 빠르게 성장하지 않도록 합니다.
이 표기법은 알고리즘 실행 시간의 상한을 표현하는 형식적인 방법입니다. 시간 복잡성의 최악의 경우 또는 작업을 완료하는 데 알고리즘의 가장 긴 시간을 측정합니다.
해당 표기법은 아래와 같이 표현됩니다:
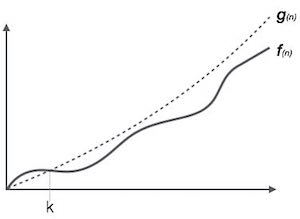
f(n) 및 g(n)가 양의 정수에 대해 정의된 두 함수인 경우
그러면 f(n) = O(g(n)) 일 때, f(n)은 g(n)의 Big oh이거나 f(n)이 g(n)의 차수이므로 상수 c가 존재하고 다음과 같은 것이 없으면 :
모든 n≥no 에 대해 f(n) ≤ c.g(n) 이라면
이는 f(n)이 g(n)보다 빠르게 성장하지 않거나 g(n)이 함수 f(n)의 상한임을 의미합니다. 이 경우 우리는 함수의 최악의 시간 복잡도, 즉 알고리즘이 얼마나 최악의 성능을 발휘할 수 있는지를 최종적으로 계산하는 함수의 성장률을 계산하고 있습니다.
예시를 통해 이해해 봅시다
예 1: f(n)=2n+3 , g(n)=n
이제 우리는 f(n)=O(g(n)) 인 것을 찾아야 합니다
f(n)=O(g(n)) 인 것을 확인하려면 다음 주어진 조건을 충족해야 합니다:
f(n)<=c.g(n)
먼저 f(n)을 2n+3으로 바꾸고 g(n)을 n으로 바꿀 것입니다.
2n+3 <= c.n
c=5, n=1이라고 가정해 봅시다
2*1+3<=5*1
5<=5
n=1 인 경우 위의 조건이 참입니다.
n=2인 경우,
2*2+3<=5*2
7<=10
n=2인 경우 위의 조건이 참입니다.
우리는 n의 모든 값에 대해 위의 조건, 즉 2n+3<=c.n을 만족 할 것이라는 것을 알고 있습니다.
만약 c의 값이 5이면 조건 2n+3<=c.n을 만족합니다. 우리는 1부터 시작하여 n의 값을 취할 수 있으며 항상 만족할 것입니다.
따라서 일부 상수 c와 일부 상수 n0에 대해 항상 2n+3<=c.n을 만족한다고 말할 수 있습니다. 위의 조건을 만족하므로 f(n)은 g(n)의 Big 0이거나 f(n)이 선형적으로 증가한다고 말할 수 있습니다. 따라서 c.g(n)이 f(n)의 상한이라는 결론이 됩니다.
다음과 같이 그래픽 적으로 나타낼 수 있습니다:
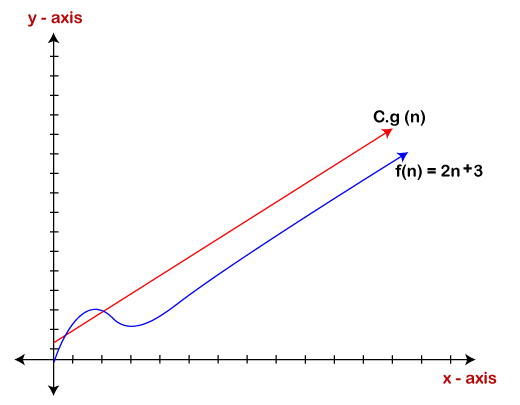
특정 함수가 2차 또는 3차 방식으로 갑자기 작동하지 않고 최악의 경우 선형 방식으로 작동한다는 확신을 제공합니다.
오메가 표기법(Ω)
- 기본적으로 big o 표기법과 반대되는 최상의 시나리오로 설명됩니다.
- 알고리즘 실행 시간의 하한을 나타내는 공식적인 방법입니다. 알고리즘이 완료하는 데 걸릴 수 있는 최상의 시간 또는 최상의 경우 시간 복잡도를 측정합니다.
- 이 표기법은 알고리즘이 실행할 수 있는 가장 빠른 시간을 결정합니다.
알고리즘이 상한을 사용하지 않고 최소한 특정 시간이 걸리도록 요구하는 경우 big-Ω 표기법, 즉 그리스 문자 "omega"를 사용합니다. 큰 입력 크기에 대한 실행 시간의 증가를 제한하는 데 사용됩니다.
f(n) 및 g(n)이 양의 정수에 대해 정의된 두 함수인 경우
그러면 f(n) = Ω (g(n))에서 f(n)은 g(n)의 오메가이거나 f(n)은 g(n)의 차수이므로 상수 c가 존재하고 다음의 경우가 아닌 경우:
모든 n≥no 및 c>0에 대해 f(n)>=c.g(n)
간단한 예를 생각해 보겠습니다:
만약 f(n) = 2n+3이면 g(n) = n,
f(n)=Ω(g(n)) 일까요?
이 식은 다음 조건을 충족해야만 합니다.
f(n)>=c.g(n)
위의 조건을 확인하기 위해 먼저 f(n)을 2n+3으로, g(n)을 n으로 바꿉니다.
2n+3>=c*n
c=1이라고 가정 한다면,
2n+3>=n (이 방정식은 1부터 시작하는 모든 n 값에 대해 참입니다).
따라서 g(n)은 2n+3 함수의 big 오메가임이 증명 됩니다.
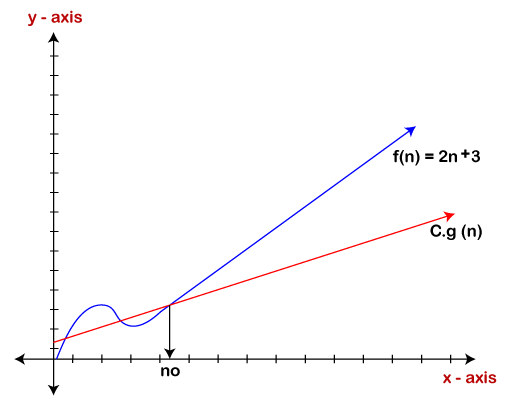
따라서 이 표기법은 가장 빠른 실행 시간을 제공합니다. 그러나 우리는 가장 빠른 실행 시간을 찾는 데 관심이 있는 것이 아니라 더 많은 작업을 수행할 수 있도록 최악의 시간이 몇 시인지 더 큰 입력에 대해 알고리즘을 확인하기를 원하기 때문에 최악의 시나리오를 계산하는 데 더 관심이 있습니다.
이 표기법은 추가 프로세스에서 추가 결정을 내리기 위해서 채택 할 수 있는 표기 입니다.
세타 표기법(θ)
- 세타 표기법은 주로 평균 사례 시나리오로 설명됩니다.
- 이 표기법은 알고리즘의 현실적인 시간 복잡도를 나타냅니다. 알고리즘이 최악 또는 최고의 경우로 수행되지 않을 때마다 실 세계의 문제의 경우 알고리즘은 주로 최악의 경우와 최상의 경우 사이에서 변동 할 것이며 이 경우 해당 표기법으로 알고리즘의 평균 사례를 찾을 수 있습니다.
- Big theta는 주로 최악의 경우와 최상의 경우의 값이 같을 때 사용합니다.
- 알고리즘 실행 시간의 상한과 하한을 모두 표현하는 공식적인 방법입니다.
빅 세타 표기법을 수학적으로 이해해 봅시다.
f(n)과 g(n)을 n의 함수라고 합시다. 여기서 n은 프로그램을 실행하는 데 필요한 단계입니다:
f(n)= θg(n)
위의 조건은 다음과 같은 경우에만 충족됩니다.
c1.g(n)<=f(n)<=c2.g(n)
여기서 함수는 2개의 극한, 즉 상한과 하한으로 제한되며 f(n)은 그 사이에 있습니다. 조건 f(n)= θg(n)은 c1.g(n)이 f(n)보다 작거나 같고 c2.g(n)이 f(n보다 크거나 같은 경우에만 참이 됩니다. ). 세타 표기법의 그래픽 표현은 다음과 같습니다:
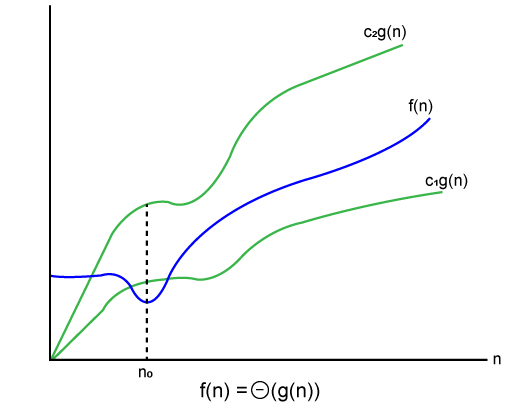
f(n)=2n+3
g(n)=n
c1.g(n)이 f(n)보다 작아야 하므로 c1은 1이어야 하고 c2.g(n)은 f(n)보다 커야 하므로 c2는 5와 같습니다. c1.g(n) 는 f(n)의 하한이고 c2.g(n)은 f(n)의 상한입니다.
c1.g(n)<=f(n)<=c2.g(n)
g(n)을 n으로 바꾸고 f(n)을 2n+3으로 바꿉니다.
c1.n <=2n+3<=c2.n
만약 c1=1, c2=2, n=1인 경우
1*1 <=2*1+3 <=2*1
1 <= 5 <= 2 // n=1인 경우 c1.g(n)<=f(n)<=c2.g(n) 조건을 만족합니다.
n=2인 경우
1*2<=2*2+3<=2*2
2<=7<=4 // n=2인 경우 c1.g(n)<=f(n)<=c2.g(n) 조건을 만족합니다.
따라서 n의 모든 값에 대해 조건 c1.g(n)<=f(n)<=c2.g(n)을 만족한다고 말할 수 있습니다. 따라서 f(n)이 g(n)의 Big 세타임이 증명됩니다. 따라서 이것은 현실적인 시간 복잡도를 제공하는 평균 사례 시나리오입니다.
세 가지 다른 점근 분석이 존재 하는 이유는 무엇일까요?
우리가 알고 있듯이 big omega는 최상의 경우이고 big oh는 최악의 경우이고 big theta는 평균적인 경우입니다. 이제 선형 검색 알고리즘의 평균, 최악 및 최상의 경우를 알아 볼 것입니다.
n개의 숫자 배열이 존재 할 떼 선형 검색을 사용하여 배열에서 특정 요소를 찾고 싶다고 가정합시다. 선형 검색에서 모든 요소는 각 반복에서 검색된 요소와 비교됩니다. (숫자의) 일치가 첫 번째 반복에서만 발견되면 최상의 경우 Ω(1)이고 요소가 마지막 요소, 즉 배열의 n번째 요소와 일치하면 최악의 경우는 O(n)이 됩니다. . 평균적인 경우는 최상과 최악의 중간이므로 θ(n/1)이 됩니다. 상수 항은 시간 복잡도에서 무시할 수 있으므로 평균 사례는 θ(n)이 됩니다.
따라서 세 가지 다른 분석을 통해 실제 함수들 간의 적절한 경계를 제공합니다. 여기서 경계는 알고리즘이 이러한 한계 사이에서만 작동하도록 보장하는 상한 및 하한이 있음을 의미합니다. 이 말은, 이러한 한계를 넘어서지 않는다는 것일 것입니다.
일반적인 점근적 표기법
|
constant
|
-
|
O(1)
|
|
linear
|
-
|
O(n)
|
|
logarithmic
|
-
|
O(log n)
|
|
n log n
|
-
|
O(n log n)
|
|
exponential
|
-
|
2^O(n)
|
|
cubic
|
-
|
O(n^3)
|
|
polynomial
|
-
|
n^O(1)
|
|
quadratic
|
-
|
O(n^2)
|
이상.
'프로그래밍' 카테고리의 다른 글
| 데이터 사이언스을 위한 C/C++ (1) | 2022.12.08 |
|---|---|
| 테스트 오케스트레이션: What, Why, and How? (0) | 2022.12.06 |
| DS Algorithm (1) | 2022.12.01 |
| 데이터 구조-소개 (0) | 2022.11.30 |
| 데이터구조에 대해서 (0) | 2022.11.29 |

