Machine learning (ML)은 산업과 학계에서 추구하는 다양한 유형의 응용과 연구 분야에서 세상을 빠르게 변화시키고 있습니다. 머신 러닝은 우리 일상 생활의 모든 부분에 영향을 미치고 있습니다. NLP와 기계 학습을 통한 음성 비서가 약속을 잡고, 달력을 확인하고, 음악을 재생하는 것에서 계획적인 광고에 이르기까지 우리가 생각하기도 전에 무엇이 필요할지 예측할 수 있을 정도로 정확합니다.
종종 머신러닝의 과학 영역의 압도적인 복잡성 때문에 정작 "그 중요한 무언가" 를 따라가는 것은 매우 도전적인 과제라는 것입니다. 하지만 기계 학습을 배우려고 하지만 이러한 개념을 처음 접하는 사람들에게 따라갈 수 있는 학습 경로를 제공할 수 있을 것입니다. 이 기사에서는 기계 학습 여정을 덜 힘들게 만드는 가장 중요한 기본 알고리즘을 살펴봅니다.
목차
머신러닝 소개.
주요 머신러닝 알고리즘.
지도 학습 대 비지도 학습.
선형 회귀.
다변수 선형 회귀.
다항식 회귀.
지수 회귀.
정현파 회귀.
대수 회귀.
머신러닝 소개.
머신러닝이란 무엇인가?
컴퓨터 프로그램은 P로 측정된 T의 작업 성능이 경험 E와 함께 향상되는 경우 일부 작업 클래스 T 및 성능 측정 P와 관련하여 경험 E로부터 학습한다고 합니다.
~ Tom M. Mitchell [1]
Source: Machine Learning Department at Carnegie Mellon
머신 러닝은 아이의 성장과 비슷한 방식으로 행동합니다. 아이가 성장함에 따라 과제 T를 수행하는 경험 E가 증가하여 더 높은 수행 척도(P)가 됩니다.
예를 들어, 우리는 아이에게 "모양 분류 블록" 장난감을 줍니다. (우리는 이 장난감이 서로 다른 다양한 모양과 해당 모양의 구멍으로 구성된다는 것을 알고 있습니다.)
이 경우 우리의 작업 T는 그 모양에 적합한 모양 구멍을 찾는 것이 될 것입니다. 그 후 아이는 모양을 관찰하고 모양의 구멍에 맞추려고 합니다. 그럼 이 장난감의 모양이 원, 삼각형, 정사각형의 세 가지라고 가정해 보겠습니다. 모양의 구멍을 찾기 위한 첫 번째 모양 찾기에서 그녀의 수행 측정(P)은 1/3이었습니다. 이 수치는 어린이가 올바른 모양의 구멍 3개 중 1개를 찾았음을 의미합니다.
두번째로, 아이는 언제 이 일을 다시 해보게 되고 그녀가 이 놀이에 약간 경험을 가지게 되었음을 알아차릴 수 있습니다. 얻은 경험(E)을 고려하여, 아이는 이 과제를 다시 시도 해보게 되어 수행(P)을 측정해보니 2/3가 되었습니다. 이 작업(T)을 100번 반복하고 난 후에 아기는 이제 어떤 모양이 어떤 모양 구멍에 들어가야하는지 알아냈습니다.
그녀의 경험(E)이 증가함에 따라 그녀의 수행(P)도 증가했으며, 우리는 이 장난감의 사용 횟수도 증가함을 발견 할 수 있었습니다. 성능도 향상되는 것은 좀 더 높은 정확도를 이끌어 내게 됩니다.
이러한 실습은 기계 학습과 비슷합니다. 기계가 하는 일이라는 것은 작업(T)을 가져와 실행하고 그에 대한 성능(P)을 측정하는 것입니다. 이제 기계에는 많은 수의 데이터가 쌓였으므로 해당 데이터를 처리할 때 시간이 지남에 따라 경험(E)이 증가하여 성능 측정(P)이 더 높아집니다. 따라서 모든 데이터를 처리하게 되면, 머신 러닝 모델의 정확도가 높아집니다. 즉, 모델에서 수행한 예측이 매우 정확해 질 것이라는 것이죠.
Arthur Samuel의 머신 러닝에 대한 또 다른 정의:
머신 러닝은 "명시적으로 프로그래밍되지 않고도 컴퓨터가 학습할 수 있는 능력"을 제공하는 컴퓨터 과학의 하위 분야입니다.-
Arthur Samuel [2]
Source: Machine Learning Department at Carnegie Mellon
이 정의를 이해하려고 노력 해 봅시다. "명시적으로 프로그래밍되지 않은 상태에서 학습"이라고 되어 있는 구문은 이는 컴퓨터에 특정 규칙 집합을 가르치지 않고 대신 컴퓨터에게 충분한 데이터를 확보하고 스스로 실수를 통해서 이를 개선하는 데 드는 학습할 시간을 제공하는 것을 의미합니다. 예를 들어, 우리는 아이에게 모양 맞추는 법을 가르쳐주지 않았지만, 같은 작업을 여러 번 반복하면서 아이 스스로 장난감에 모양을 맞추는 법을 배웠습니다.
따라서 우리는 어린이에게 모양을 맞추는 방법을 명시 적으로 가르치지 않았다고 말할 수 있습니다. 우리는 기계로 똑같은 일을 합니다. 작업하기에 충분한 데이터를 제공하고 우리가 거기서 원하는 정보를 제공합니다. 따라서 데이터를 처리하고 그 데이터를 정확하게 예측합니다.
머신러닝은 왜 필요 한가?
예를 들어 고양이와 개 이미지 집합이 있다고 합시다. 이것들을 고양이와 개 그룹으로 분류하고 싶어 하는 것이 우리가 원하는 것입니다. 그러기 위해서는 다음과 같은 다양한 동물의 특성을 찾아야 합니다:
각 동물의 눈은 몇 개일까?
각 동물의 눈 색깔은 무엇일까?
각 동물의 키는 얼마일까?
각 동물의 무게는 얼마일까?
각 동물은 일반적으로 무엇을 먹을까?
우리는 이러한 각 질문의 답변에 대한 벡터를 구성합니다.
그런 다음 다음과 같은 일련의 규칙을 적용합니다.
If height > 1 feet and weight > 15 lbs, then it could be a cat.
https://pub.towardsai.net/machine-learning-algorithms-for-beginners-with-python-code-examples-ml-19c6afd60daa
이제 모든 데이터 포인트에 대해 이러한 규칙 집합을 만들어야 합니다. 또한 if, else if, else 문의 결정 트리를 배치하고 어느 범주 중 하나에 속하는지 확인합니다.
우리에게 머신러닝을 사용 할 수 있는 환상적인 기회를 주기위해서 이 실험의 결과가 많은 동물을 잘못 분류하여 결과가 좋지 않았다고 가정해 보겠습니다.
기계 학습이 하는 일은 다양한 종류의 알고리즘으로 데이터를 처리하여 고양이인지 개인지를 판별하는 데 어떤 특성이 더 중요한지 알려줍니다. 그렇게되면 많은 규칙 집합을 적용하는 대신 두세 가지 특성을 기반으로 단순화할 수 있으며 결과적으로 더 높은 정확도를 제공해 줄 것입니다. 이전 방법은 예측을 할 만큼 충분히 일반화되지 않았었습니다.
기계 학습 모델은 다음과 같은 많은 작업에서 우리를 돕습니다.
객체 인식
요약
예측
분류
클러스터링
추천 시스템
그리고 여러가지 것들
머신러닝 모델은 무엇인가?
기계 학습 모델은 기계 학습 관련 작업을 처리하는 질문/응답 시스템입니다. 문제를 풀 때 데이터를 표현하는 알고리즘 시스템으로 생각해 볼 수 있습니다. 아래에서 다룰 방법은 비즈니스 문제를 해결하기 위한 산업 관련 목적에 유용합니다.
예를 들어, 우리가 Google Adwords의 ML 시스템에서 작업 중이고 우리의 작업은 데이터를 사용하여 특정 인구통계 또는 영역을 전달하기 위해 ML 알고리즘을 구현하는 것이라고 가정해 보겠습니다. 이러한 작업은 데이터를 사용하여 비즈니스 결과를 개선하기 위한 귀중한 통찰력을 수집하는 것이 목적입니다.
주요 머신러닝 알고리즘들:
1. Regression (Prediction) 회귀(예측)
우리는 일련의 연속 된 값들을 예측하는 데 #회귀 알고리즘을 사용합니다.
#회귀알고리즘들:
Linear Regression
Polynomial Regression
Exponential Regression
Logistic Regression
Logarithmic Regression2. 분류
항목의 등급 또는 범주 집합을 예측하기 위해 분류 알고리즘을 사용합니다.
#분류알고리즘 :
K-Nearest Neighbors
Decision Trees
Random Forest
Support Vector Machine
Naive Bayes3. 클러스터링
우리는 데이터를 요약하거나 구조화하기 위해 클러스터링 알고리즘을 사용합니다.
#클러스터링알고리즘 :
K-means
DBSCAN
Mean Shift
Hierarchical4. 연관
우리는 동시에 발생하는 항목이나 이벤트를 연결하기 위해 연결 알고리즘을 사용합니다.
연관 알고리즘:
Apriori
5. 이상 감지
우리는 비정상적인 활동과 사기 탐지와 같은 비정상적인 경우를 발견하기 위해 이상 탐지를 사용합니다.
6. 시퀀스 패턴 마이닝
우리는 시퀀스의 데이터 예제 사이의 다음 데이터 이벤트를 예측하기 위해 순차적 패턴 마이닝을 사용합니다.
7. 차원축소
데이터 집합에서 유용한 기능만 추출하기 위해 데이터 크기를 줄이기 위해 차원 축소를 사용합니다
8. 추천시스템
추천 엔진을 구축하기 위해 추천 알고리즘을 사용합니다.
예:
넷플릭스 추천 시스템.
책 추천 시스템.
아마존 제품 추천 시스템.
오늘날, 우리는 인공지능, 머신러닝, 딥러닝 그리고 여러가지 용어 같은 복잡한 용어들을 듣고 있습니다.
인공 지능, 기계 학습 및 딥 러닝의 근본적인 차이점은 무엇일까요?
인공지능 (AI):
Andrew Moore 교수가 정의한 인공 지능(AI)은 최근까지 인간의 지능이 필요하다고 생각했던 방식으로 컴퓨터가 작동하도록 하는 과학 및 공학입니다[4].
여기에는 다음과 같은 분야를 포함합니다.
Computer Vision
Language Processing
Creativity
Summarization머신러닝 (ML):
톰 미첼(Tom Mitchell) 교수가 정의한 바와 같이 머신 러닝은 경험을 통해 컴퓨터 프로그램이 자동으로 개선될 수 있도록 하는 컴퓨터 알고리즘 연구에 중점을 둔 AI의 과학 분야를 의미합니다[3].
여기에는 다음이 포함됩니다.
분류
신경망
클러스터링딥 러닝:
딥 러닝은 높은 컴퓨팅 성능 및 대규모 데이터 세트와 결합된 계층화된 신경망이 강력한 기계 학습 모델을 생성할 수 있는 기계 학습의 하위 집합입니다. [3]

우리는 왜 기계 학습 알고리즘을 Python으로 구현 하려 할까요?
Python은 널리 사용되는 범용 프로그래밍 언어입니다. Python을 사용하여 기계 학습 알고리즘을 작성할 수 있으며 잘 작동합니다. 파이썬이 데이터 과학자들 사이에서 인기를 얻는 이유는 파이썬에는 우리의 삶을 더 편안하게 해주는 다양한 모듈과 라이브러리가 이미 구현되어 있기 때문입니다.
흥미로운 Python 라이브러리에 대해 간략히 살펴보겠습니다.
#Numpy : Python에서 n차원 배열로 작업하는 수학 라이브러리입니다. 계산을 효과적이고 효율적으로 수행할 수 있습니다.
#Scipy : 신호 처리, 최적화, 통계 등을 포함하는 수치 알고리즘 및 도메인별 도구 상자 모음입니다. Scipy는 과학 및 고성능 계산을 위한 기능 라이브러리입니다.
#Matplotlib : 2D 플로팅과 3D 플로팅을 모두 제공하는 트렌디한 플로팅 패키지입니다.
Scikit-learn: 파이썬 프로그래밍 언어를 위한 무료 기계 학습 라이브러리입니다. 분류, 회귀 및 클러스터링 알고리즘의 대부분을 가지고 있으며 Numpy, Scipy와 같은 Python 수치 라이브러리와 함께 작동합니다.
기계 학습 알고리즘은 두 그룹으로 분류됩니다.
|
지도 학습 알고리즘
비지도 학습 알고리즘 |
I. 지도 학습 알고리즘:
목적: 클래스 또는 값 레이블을 예측합니다.
지도 학습은 레이블이 지정된 학습 데이터에서 기능을 추론하는 것과 관련된 기계 학습의 한 가지입니다(현재는 기계/딥 러닝의 주류). 훈련 데이터는 *(input, target)* 쌍의 집합으로 구성되며, 여기서 입력은 특성 벡터가 될 수 있고 target은 함수가 출력하기를 원하는 것을 지시합니다. *target*의 유형에 따라 지도 학습을 분류와 회귀의 두 가지 범주로 대략 나눌 수 있습니다.
분류에는 범주별 대상이 포함됩니다. 이미지 분류와 같은 간단한 경우부터 기계 번역 및 이미지 캡션과 같은 고급 주제에 이르기까지 다양한 예가 있습니다. 회귀에는 연속 대상이 포함됩니다. 그 응용 프로그램에는 주식 예측, 이미지 마스킹 및 기타가 포함되며 모두 이 범주에 속합니다.

지도 학습이 무엇인지 이해하기 위해 예제를 사용 할 것입니다. 예를 들어, 우리는 어린이에게 10마리의 사자, 10마리의 원숭이, 10마리의 코끼리 등 각 종류별 동물 10마리 씩 있는 박제 동물 100개를 줍니다. 그런 다음, 우리는 아이들이 동물의 다른 특성(특성)에 따라 다양한 유형의 동물을 구별할 수 있도록 가르칩니다. 예를 들어 색깔이 주황색이면 사자일 수도 있습니다. 몸통이 있는 큰 동물이라면 코끼리일 수 있습니다.
우리는 아이에게 동물을 구별하는 방법을 가르칩니다. 이것은 감독 학습의 예가 될 수 있습니다. 이제 우리가 아이에게 다양한 동물을 가리킬 때 아이는 적절한 동물 그룹으로 분류할 수 있어야 합니다.
이 예에서는 아이가 분류 한 것 중 8/10이 맞았음을 알 수 있었습니다. 그래서 우리는 그 아이가 꽤 잘했다고 말할 수 있습니다. 이는 컴퓨터에도 동일하게 적용됩니다. 우리는 그들에게 실제 레이블이 지정된 값과 함께 수천 개의 데이터 포인트를 제공합니다(레이블이 있는 데이터는 특성 값과 함께 데이터를 다양한 그룹으로 분류합니다). 그런 다음 훈련 기간 동안 다양한 특성에서 학습합니다. 훈련 기간이 끝나면 훈련된 모델을 사용하여 예측할 수 있습니다. 우리는 이미 레이블이 지정된 데이터를 머신에 제공했기 때문에 예측 알고리즘이 지도 학습을 기반으로 했다는 것을 염두에 두십시오. 간단히 말해서 이 예의 예측은 레이블이 지정된 데이터를 기반으로 한다고 말할 수 있습니다.
지도 학습 알고리즘의 예:
|
선형 회귀
로지스틱 회귀 K-가장 가까운 이웃 의사결정나무 랜덤 포레스트 서포트 벡터 머신 |
II. 비지도 학습:
목적: 데이터 패턴/그룹화 결정.
지도 학습과 대조적입니다. 비지도 학습은 데이터의 숨겨진 구조를 설명하는 함수인 레이블이 지정되지 않은 데이터에서 추론하게 됩니다.
아마도 가장 기본적인 비지도 학습 유형은 PCA, t-SNE와 같은 차원 축소 방법이며 PCA는 일반적으로 데이터 전처리에 사용되며 t-SNE는 일반적으로 데이터 시각화에 사용됩니다.
더 발전된 분기는 데이터의 숨겨진 패턴을 탐색한 다음 예측을 수행하는 클러스터링입니다. 예를 들면 K-평균 클러스터링, 가우스 혼합 모델, 은닉 마르코프 모델 등이 있습니다.
딥 러닝의 르네상스와 함께 비지도 학습은 수동으로 데이터에 레이블을 지정하지 않아도 되므로 점점 더 많은 관심을 받고 있습니다. 딥 러닝의 관점에서 우리는 두 종류의 비지도 학습, 즉 표현 학습과 생성 모델을 고려합니다.
표현 학습은 일부 다운스트림 작업에 유용한 상위 수준의 대표 특성을 추출하는 것을 목표로 하는 반면 생성 모델은 일부 숨겨진 매개변수에서 입력 데이터를 재현하는 목적입니다.

비지도 학습은 글자그대로 동작하는 것입니다. 이러한 유형의 알고리즘에는 레이블이 지정된 데이터가 없습니다. 따라서 기계는 입력 데이터를 처리하고 출력에 대한 결론을 내려야 합니다. 예를 들어, 우리가 모양 장난감을 준 아이를 기억하십니까? 이 경우 그는 다른 모양에 대한 완벽한 모양 구멍을 찾기 위해 자신의 실수에서 배워야 할 것입니다.
그러나 문제는 우리가 (레이블이 있는 데이터라고 하는 기계 학습 목적을 위해) 모양에 맞추는 방법을 가르쳐주어서 아이가 행동하도록 하지 않는다는 것입니다. 그러나 아이는 장난감의 다양한 특성에서 배우게되고 이것을 바탕으로 결론을 내리려고 할 것입니다.
요컨대, 예측은 레이블이 지정되지 않은 데이터를 기반으로 합니다.
비지도 학습 알고리즘의 예:
|
Dimension Reduction
Density Estimation Market Basket Analysis Generative adversarial networks (GANs) Clustering |
1. 선형 회귀
#선형회귀 는 입력 특성과 출력 간의 관계를 모델링하는 통계적 접근 방식입니다. 입력된 특성을 독립변수라고 하고 출력을 종속변수라고 합니다. 여기서 우리의 목표는 입력 특성을 최적 계수와 곱한 것을 기반으로 출력 값을 예측하는 것입니다.
선형 회귀의 실제 예:
|
(1) 제품의 판매를 예측하기 위해.
(2) 경제 성장을 예측하기 위해. (3) 석유 가격을 예측하기 위해. (4) 새 차의 배출가스 예측을 위해. (5) GPA가 대학 입학에 미치는 영향. |
두 가지 유형의 선형 회귀가 있습니다.
|
단순 선형 회귀
다변수 선형 회귀 |
1.1 단순 선형 회귀
단순 선형 회귀에서는 하나의 입력 특성만을 기반으로 출력/종속 변수를 예측합니다. 단순 선형 회귀의 식은 다음과 같습니다.

아래 예제는 파이썬 sklearn 라이브러리를 이용해서 단순 선형회귀를 구현할 예제 입니다.
단계별 파이썬 구현
a. 라이브러리 임포트:
계산을 위해서 여러가지 라이브러리를 사용할 것이므로, 다음을 임포트 하여야 합니다.
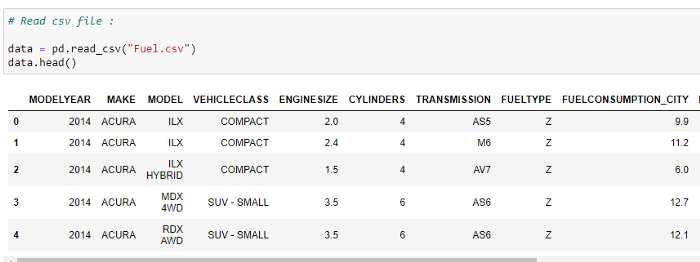
b. CSV 파일 읽기:
데이터 세트의 처음 5개 행을 확인합니다. 이 예에서 우리는 차량 모델 데이터 집합를 사용하고 있습니다. Softlayer IBM에서 데이터 세트를 확인하십시오.
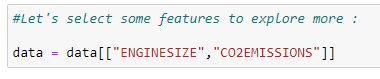
c. 우리가 예측할 값으로 고려해야 할 특성을 선택하십시오.
여기서 우리의 목표는 데이터 집합의 "engine size(엔진 크기)" 값으로부터 "co2 emissions(이산화탄소 배출량)" 값을 예측하는 것입니다.
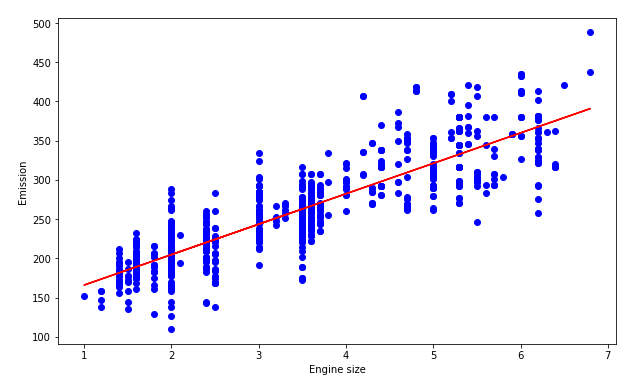
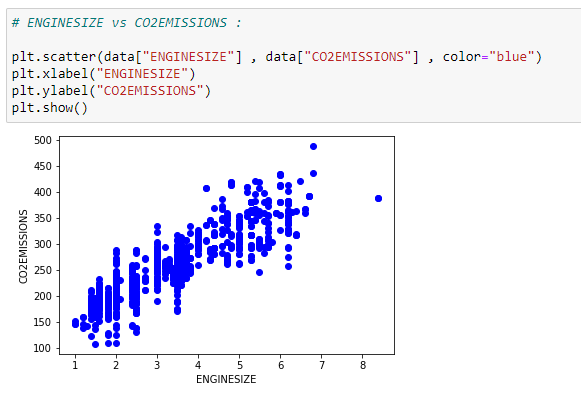
d. 데이터 표시하기
우리는 데이터를 산점도 플롯으로 그려볼수 있습니다.
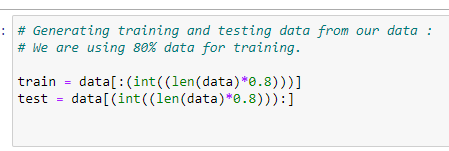
e. 데이터를 훈련과 테스트 데이터로 나누기:
모델의 정확도를 확인하기 위해 데이터를 훈련 데이터 집합과 테스트 데이터 집합으로 나눌 것입니다. 훈련 데이터를 사용하여 모델을 훈련한 다음 테스트 데이터 집합을 사용하여 모델의 정확도를 확인할 것입니다.
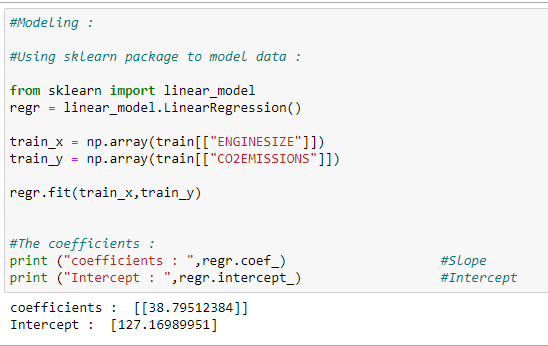
f. 모델 훈련하기:
우리의 모델을 훈련하고 최적 회귀 선을 위한 계수를 찾는 법을 구현한 코드 입니다.
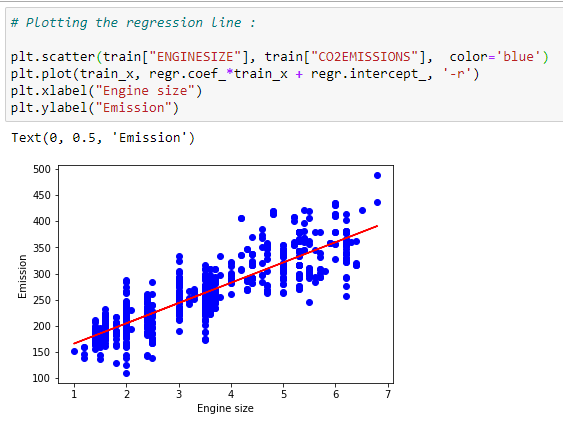
g. 최적 선 표시하기:
계수를 근간으로, 우리는 우리 데이터 집합의 최적 선을 그려 볼 수 있습니다.
h. 예측함수:
우리는 테스트 데이터 집합에 예측 함수를 사용 할 것입니다.

i. 이산화 탄소 배출량 예측하기:
이 회귀 선을 바탕으로 이산화탄소 배출량 값을 예측 합니다.
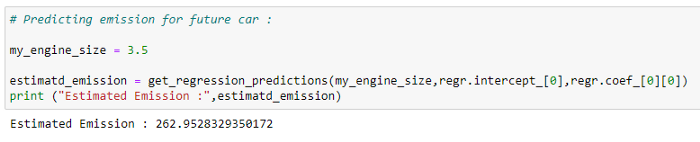
j. 테스트 데이터에 대한 정확도 확인:
우리는 우리의 데이터 집합에서 예측 된 값들을 실제 값들과 비교 해 봄으로써 모델의 정확도를 확인 할 수 있습니다.
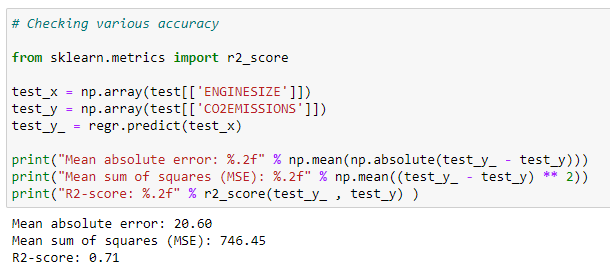
한데 모아보기:
# Import required libraries:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# Read the CSV file :
data = pd.read_csv(“Fuel.csv”)
data.head()
# Let’s select some features to explore more :
data = data[[“ENGINESIZE”,”CO2EMISSIONS”]]
# ENGINESIZE vs CO2EMISSIONS:
plt.scatter(data[“ENGINESIZE”] , data[“CO2EMISSIONS”] , color=”blue”)
plt.xlabel(“ENGINESIZE”)
plt.ylabel(“CO2EMISSIONS”)
plt.show()
# Generating training and testing data from our data:
# We are using 80% data for training.
train = data[:(int((len(data)*0.8)))]
test = data[(int((len(data)*0.8))):]
# Modeling:
# Using sklearn package to model data :
regr = linear_model.LinearRegression()
train_x = np.array(train[[“ENGINESIZE”]])
train_y = np.array(train[[“CO2EMISSIONS”]])
regr.fit(train_x,train_y)
# The coefficients:
print (“coefficients : “,regr.coef_) #Slope
print (“Intercept : “,regr.intercept_) #Intercept
# Plotting the regression line:
plt.scatter(train[“ENGINESIZE”], train[“CO2EMISSIONS”], color=’blue’)
plt.plot(train_x, regr.coef_*train_x + regr.intercept_, ‘-r’)
plt.xlabel(“Engine size”)
plt.ylabel(“Emission”)
# Predicting values:
# Function for predicting future values :
def get_regression_predictions(input_features,intercept,slope):
predicted_values = input_features*slope + intercept
return predicted_values
# Predicting emission for future car:
my_engine_size = 3.5
estimatd_emission = get_regression_predictions(my_engine_size,regr.intercept_[0],regr.coef_[0][0])
print (“Estimated Emission :”,estimatd_emission)
# Checking various accuracy:
from sklearn.metrics import r2_score
test_x = np.array(test[[‘ENGINESIZE’]])
test_y = np.array(test[[‘CO2EMISSIONS’]])
test_y_ = regr.predict(test_x)
print(“Mean absolute error: %.2f” % np.mean(np.absolute(test_y_ — test_y)))
print(“Mean sum of squares (MSE): %.2f” % np.mean((test_y_ — test_y) ** 2))
print(“R2-score: %.2f” % r2_score(test_y_ , test_y) )1.2 다변수 선형회귀:
단순 선형 회귀에서는 출력 특성의 값을 예측하기 위해 하나의 입력 특성만 고려할 수 있었습니다. 그러나 다변수 선형 회귀에서는 둘 이상의 입력 특성을 기반으로 출력을 예측할 수 있습니다. 다음은 다변수 선형 회귀 공식입니다.

단계별 구현(파이썬):
a. 필수 라이브러리 임포트:
b. CSV 파일 읽기:
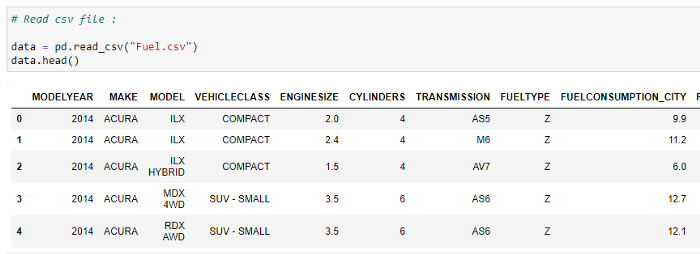
c. X와 Y 값 정의하기:
X는 우리가 생각하는 입력 특성을 저장하고, Y는 출력 값을 저장 합니다.

d. 테스트와 훈련 데이터집함으로 데이터를 나누기:
여기서 80% 는 훈련용, 20% 데이터는 테스트 용으로 사용할 것입니다.
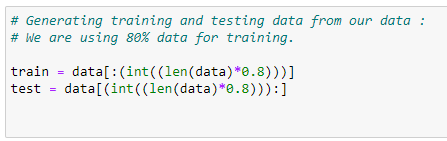
e. 모델 훈련하기:
여기에서 데이터의 80%를 사용해서 우리 모델을 훈련 할 것입니다.
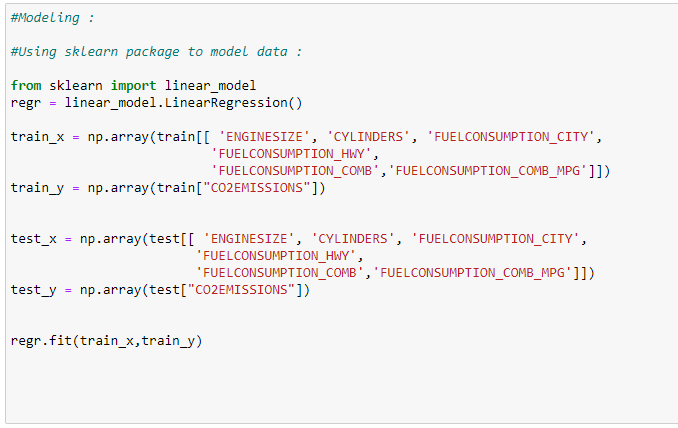
f. 입력 특성의 계수 찾기:
이제 어떤 특성이 출력 변수에 더 중요한 영향을 미치는지 알아야 할 필요가 있습니다. 이를 위해 계수 값을 인쇄할 것입니다.
계수가 음수라는 것는 출력에 역효과가 있음을 의미합니다. 즉, 해당 기능의 값이 증가하면 출력 값은 감소합니다.
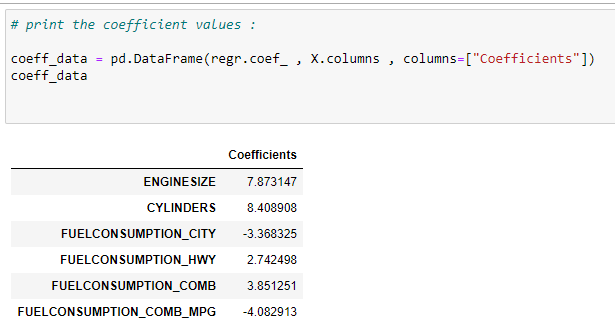
g. 값 예측:
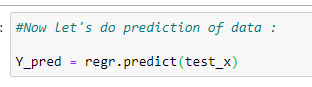
h. 모델의 정확도:
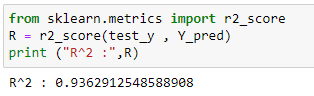
이제 여기에서 단순 및 다변수 선형 회귀에 대해 동일한 데이터 집합를 사용했음에 주목하십시오. 다변수 선형 회귀의 정확도가 단순 선형 회귀의 정확도보다 훨씬 우수함을 알 수 있습니다.
모두 모아보기:
# Import the required libraries:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# Read the CSV file:
data = pd.read_csv(“Fuel.csv”)
data.head()
# Consider features we want to work on:
X = data[[ ‘ENGINESIZE’, ‘CYLINDERS’, ‘FUELCONSUMPTION_CITY’,’FUELCONSUMPTION_HWY’,
‘FUELCONSUMPTION_COMB’,’FUELCONSUMPTION_COMB_MPG’]]
Y = data[“CO2EMISSIONS”]
# Generating training and testing data from our data:
# We are using 80% data for training.
train = data[:(int((len(data)*0.8)))]
test = data[(int((len(data)*0.8))):]
#Modeling:
#Using sklearn package to model data :
regr = linear_model.LinearRegression()
train_x = np.array(train[[ ‘ENGINESIZE’, ‘CYLINDERS’, ‘FUELCONSUMPTION_CITY’,
‘FUELCONSUMPTION_HWY’, ‘FUELCONSUMPTION_COMB’,’FUELCONSUMPTION_COMB_MPG’]])
train_y = np.array(train[“CO2EMISSIONS”])
regr.fit(train_x,train_y)
test_x = np.array(test[[ ‘ENGINESIZE’, ‘CYLINDERS’, ‘FUELCONSUMPTION_CITY’,
‘FUELCONSUMPTION_HWY’, ‘FUELCONSUMPTION_COMB’,’FUELCONSUMPTION_COMB_MPG’]])
test_y = np.array(test[“CO2EMISSIONS”])
# print the coefficient values:
coeff_data = pd.DataFrame(regr.coef_ , X.columns , columns=[“Coefficients”])
coeff_data
#Now let’s do prediction of data:
Y_pred = regr.predict(test_x)
# Check accuracy:
from sklearn.metrics import r2_score
R = r2_score(test_y , Y_pred)
print (“R² :”,R)1.3 다항식 회귀:
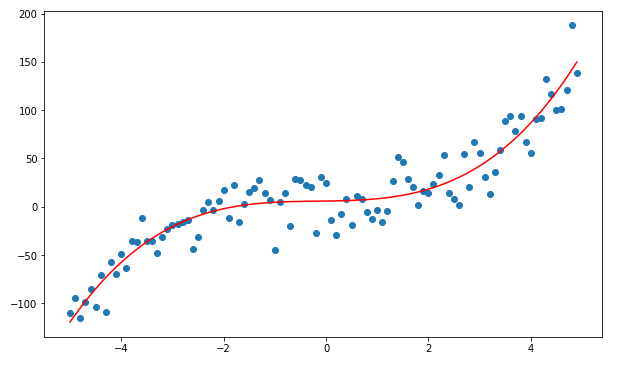
때로는 선형 추세를 따르지 않는 데이터를 가지고 있을 수 있습니다. 때로는 다항식 추세를 따르는 데이터가 가지고 있을 수 있습니다. 그래서 우리는 다항식 회귀를 사용할 것입니다.
구현에 들어가기 전에, 일부 기본 다항식 데이터의 그래프가 어떻게 보이는지 알아야 합니다.
다항식 함수 및 해당 그래프:
a. Y=X 그래프
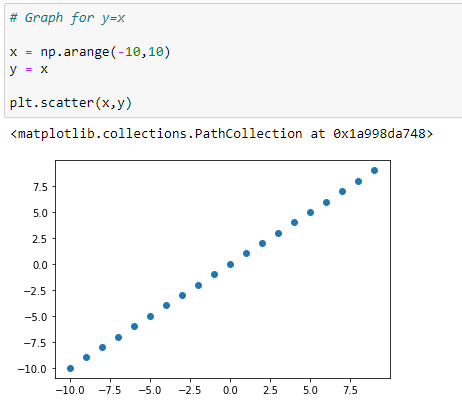
b. Y=X² 그래프:
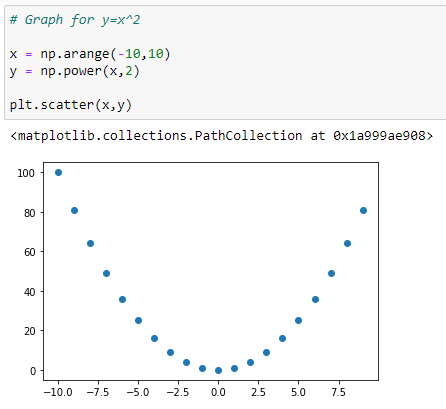
c. Y=X³ 그래프:
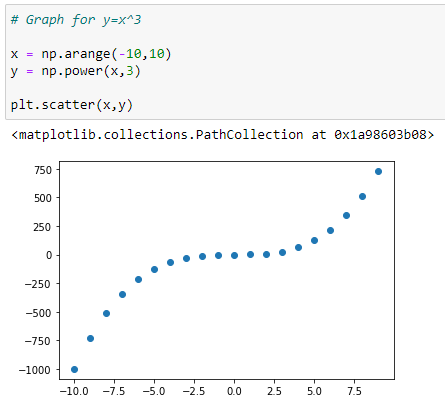
d. 하나 이상의 다항식을 가지는 그래프: Y = X³+X²+X:
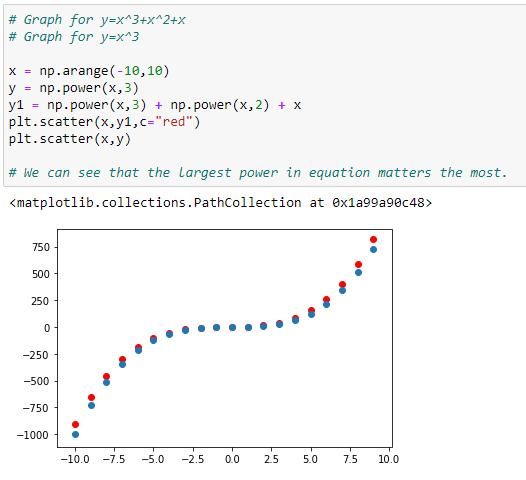
위의 그래프에서 빨간색 점은 Y=X³+X²+X에 대한 그래프를 나타내고 파란색 점은 Y=X³에 대한 그래프를 나타냅니다.
여기에서 가장 큰 거듭 제곱값이 그래프의 모양에 영향을 미친다는 것을 알 수 있습니다.
다음은 다항식 회귀 공식입니다.

이제 이전 회귀 모델에서 구현을 위해 sci-kit 학습 라이브러리를 사용했습니다.
이제 정규식( Normal Equation)을 사용하여 구현하겠습니다. 여기에서 다항식 회귀를 구현하는 데 scikit-learn을 사용할 수도 있지만 다른 방법을 사용해 보면 작동 방식에 대한 통찰력을 얻을 수 있습니다.
방정식은 다음과 같습니다.
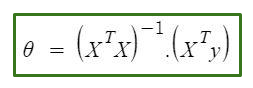
위의 방정식에서:
θ: 방정식을 가장 잘 정의하는 가설 매개변수.
X: 각 인스턴스의 특성 입력 값.
Y: 각 인스턴스의 출력 값.
1.3.1 다항식 회귀를 위한 가설 함수
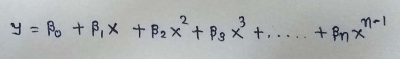
표준 방정식 내의 주요 행렬
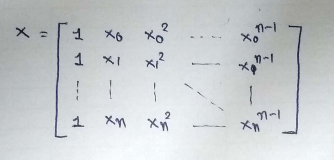
파이썬으로 단계별 구현하기:
a. 필요 라이브러리 임포트:
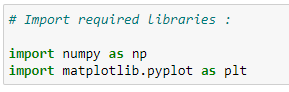
b. 데이터 포인트 생성하기:
다항식 회귀를 구현하기 위한 데이터 집합 생성하기.
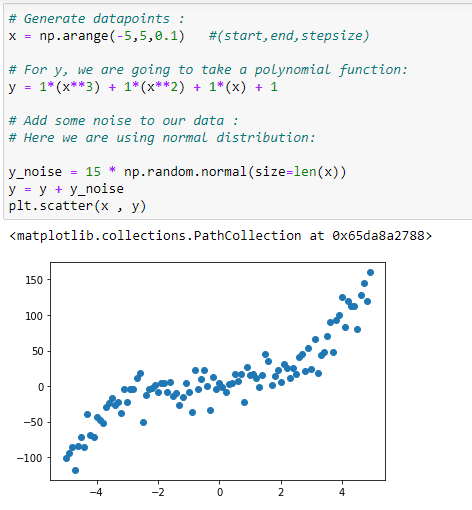
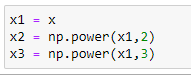
c. x,x²,x³ 벡터 초기화:
x의 3승으로 최대 값을 가지도록합니다.
따라서 우리의 X 행렬은 X, X², X³ 을 가지게 될 것입니다.
d. X 행렬의 첫번째 컬럼
주 행렬 X의 첫 번째 열은 beta_0의 계수를 유지하기 때문에 항상 1입니다.
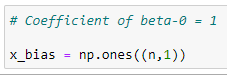
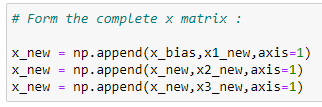
e. x 행렬 형태 완성하기:
구현의 시작부에서 X 행렬을 살펴봅시다. 우리는 여기에 벡터를 추가 하여 생성 하도록 합니다.
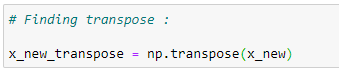
f. 행렬의 전차:
우리는 단계적으로 세타 값을 계산 할 것입니다.
첫번째로, 우리는 행렬의 전차를 구해야 합니다.
g. 행렬 곱:
전차를 구했으면 원 행렬에 이 값을 곱할 필요가 있습니다.
정규식으로 다항식 회귀를 구할 예정임을 명심하고 보면, 그래서 다음 규칙에 따라야 합니다.

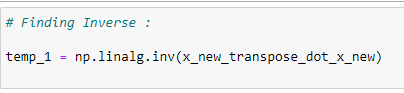
h. 행렬의 역행렬:
행렬의 역행렬을 구한다음 temp1에 이 행렬을 저장합니다.
i. 행렬 곱:
전차 X와 Y 벡터를 곱하여 temp2 변수에 저장합니다.
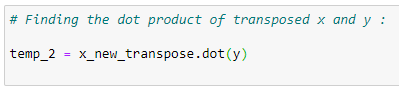
j. Coefficient values:
계수 값 찾기
To find the coefficient values, we need to multiply temp1 and temp2. See the Normal Equation formula.
계수 값을 찾기 위해서 우리는 temp1과 temp2를 곱합니다.
정규 방정식 공식을 참고 합시다.
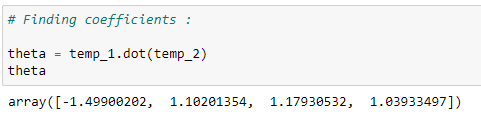
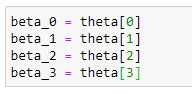
k. Store the coefficients in variables:
값들의 계수들 저장하기
Storing those coefficient values in different variables.
서로 다른 값들에 대한 이 값들의 계수를 저장합니다.
l. 데이터 곡선 표시하기
회귀 곡선 데이터를 표시 해 봅니다.
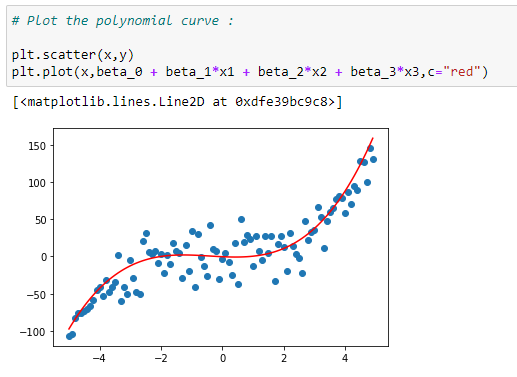
m. 예측함수:
이 회귀 곡선을 사용해서 출력 값을 예측 해 볼 것입니다.
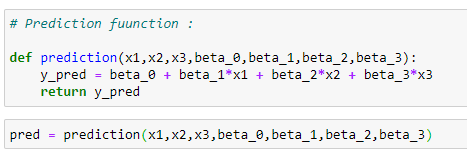
n. 오류 함수:
평균 제곱 오차 함수를 사용하여 오차를 계산합니다.

o. 오류율 계산하기:
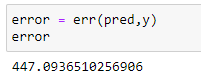
한데 모아보기
# Import required libraries:
import numpy as np
import matplotlib.pyplot as plt
# Generate datapoints:
x = np.arange(-5,5,0.1)
y_noise = 20 * np.random.normal(size = len(x))
y = 1*(x**3) + 1*(x**2) + 1*x + 3+y_noise
plt.scatter(x,y)
# Make polynomial data:
x1 = x
x2 = np.power(x1,2)
x3 = np.power(x1,3)
# Reshaping data:
x1_new = np.reshape(x1,(n,1))
x2_new = np.reshape(x2,(n,1))
x3_new = np.reshape(x3,(n,1))
# First column of matrix X:
x_bias = np.ones((n,1))
# Form the complete x matrix:
x_new = np.append(x_bias,x1_new,axis=1)
x_new = np.append(x_new,x2_new,axis=1)
x_new = np.append(x_new,x3_new,axis=1)
# Finding transpose:
x_new_transpose = np.transpose(x_new)
# Finding dot product of original and transposed matrix :
x_new_transpose_dot_x_new = x_new_transpose.dot(x_new)
# Finding Inverse:
temp_1 = np.linalg.inv(x_new_transpose_dot_x_new)# Finding the dot product of transposed x and y :
temp_2 = x_new_transpose.dot(y)
# Finding coefficients:
theta = temp_1.dot(temp_2)
theta
# Store coefficient values in different variables:
beta_0 = theta[0]
beta_1 = theta[1]
beta_2 = theta[2]
beta_3 = theta[3]
# Plot the polynomial curve:
plt.scatter(x,y)
plt.plot(x,beta_0 + beta_1*x1 + beta_2*x2 + beta_3*x3,c=”red”)
# Prediction function:
def prediction(x1,x2,x3,beta_0,beta_1,beta_2,beta_3):
y_pred = beta_0 + beta_1*x1 + beta_2*x2 + beta_3*x3
return y_pred
# Making predictions:
pred = prediction(x1,x2,x3,beta_0,beta_1,beta_2,beta_3)
# Calculate accuracy of model:
def err(y_pred,y):
var = (y — y_pred)
var = var*var
n = len(var)
MSE = var.sum()
MSE = MSE/n
return MSE
# Calculating the error:
error = err(pred,y)
error1.4 지수 회귀:
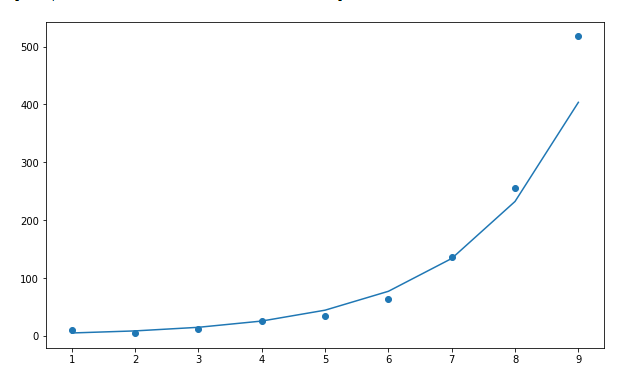
지수 성장의 실세계 예제:
1. Microorganisms in cultures.
2. 식품의 부패.
3. 인구.
4. 복리 이자.
5. 전염병(예: 코로나19).
6. 에볼라 전염병.
7. 외래 침입종.
8. 산불.
9. 암세포.
10. 스마트폰 보급 및 판매.
지수 회귀 공식은 다음과 같습니다.

이 경우, 우리는 a, b, c 같은 계수 값을 찾기 위해서 scikit-learn 라이브러리를 사용 할 것입니다.
파이썬의 단계별 구현
a. 필요 라이브러리 임포트:
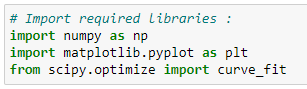
b. 데이터포인트 추가:

c. 지수 함수 알고리즘 구현:
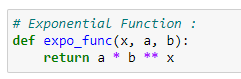
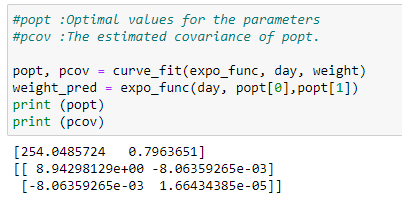
d. 최적 매개변수 적용 및 공분산:
여기에서 최적의 매개변수 값을 찾기 위해 curve_fit을 사용합니다. 함수는 popt, pcov라는 두 개의 변수를 반환합니다.
popt는 최적 매개변수들의 값을 저장하고 pcov는 공분산의 값을 저장합니다.
pop 변수에 두 개의 값이 들어 있음을 알 수 있습니다. 이 값들이 우리가 찾는 최적의 매개변수입니다.
아래와 같이 이 매개변수들을 사용하여 최적의 곡선을 그릴 것입니다.
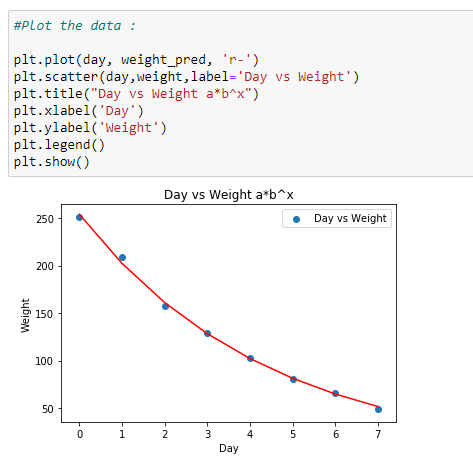
e. 데이터 표시하기:
찾은 계수를 이용하여 데이터를 표시 합니다.
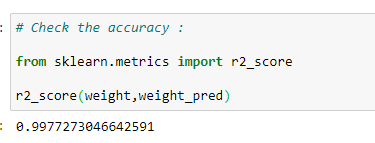
f. 모델의 정확도 확인하기:
r2_score로 모델의 정확도를 확인합니다.
한데 모아보기
# Import required libraries:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# Dataset values :
day = np.arange(0,8)
weight = np.array([251,209,157,129,103,81,66,49])
# Exponential Function :
def expo_func(x, a, b):
return a * b ** x
#popt :Optimal values for the parameters
#pcov :The estimated covariance of popt
popt, pcov = curve_fit(expo_func, day, weight)
weight_pred = expo_func(day,popt[0],popt[1])
# Plotting the data
plt.plot(day, weight_pred, ‘r-’)
plt.scatter(day,weight,label=’Day vs Weight’)
plt.title(“Day vs Weight a*b^x”)
plt.xlabel(‘Day’)
plt.ylabel(‘Weight’)
plt.legend()
plt.show()
# Equation
a=popt[0].round(4)
b=popt[1].round(4)
print(f’The equation of regression line is y={a}*{b}^x’)1.5 정현파 회귀:
정현파 회귀의 몇 가지 실제 예:
음악 파형의 생성.
소리는 파형의 이동입니다.
구조의 삼각 함수.
우주 비행에 사용됩니다.
GPS 위치 계산.
건축학.
전류.
라디오 방송.
바다의 밀물과 썰물.
건물.
때때로 사인파와 같은 패턴을 보여주는 데이터가 있습니다. 따라서 이러한 경우에는 사인 곡선 회귀를 사용합니다. 아래에 알고리즘 공식을 표시할 수 있습니다.:

단계별 파이썬 구현
a. 데이터집합 생성하기:
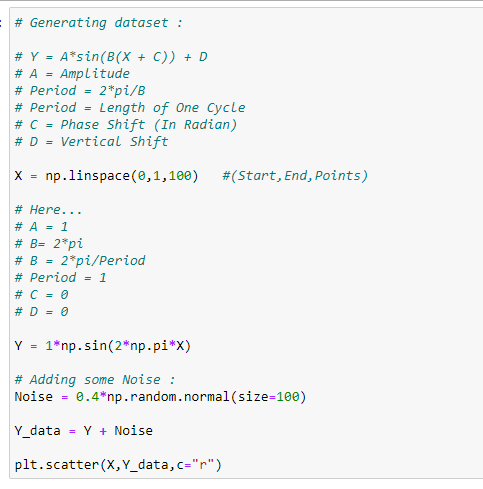
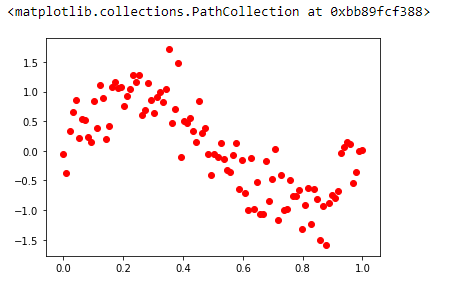
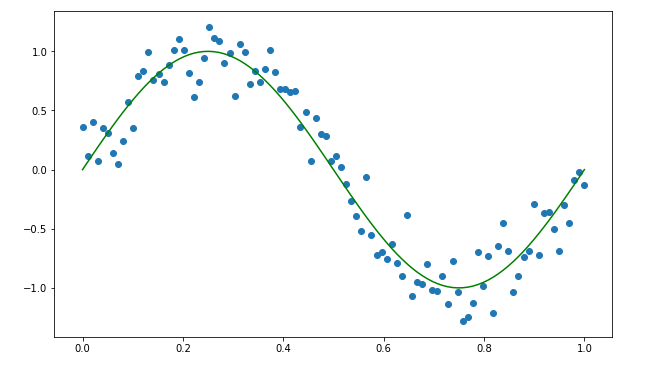
b. 사인 함수 적용하기:
여기에서 최적 계수를 기반으로 출력 값을 계산하기 위해 "calc_sine"이라는 함수를 만들었습니다. 여기서는 scikit-learn 라이브러리를 사용하여 최적의 매개변수를 찾습니다.
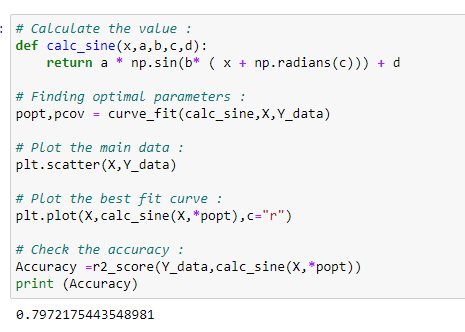
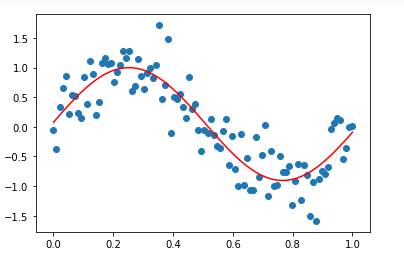
c. 선형 회귀보다 정현파 회귀가 좀 더 좋은 성능을 낼까요?
데이터를 직선으로 피팅한 후 모델의 정확도를 확인하면 예측 정확도가 사인파 회귀보다 떨어지는 것을 알 수 있습니다. 이것이 사인파 회귀를 사용하는 이유입니다.
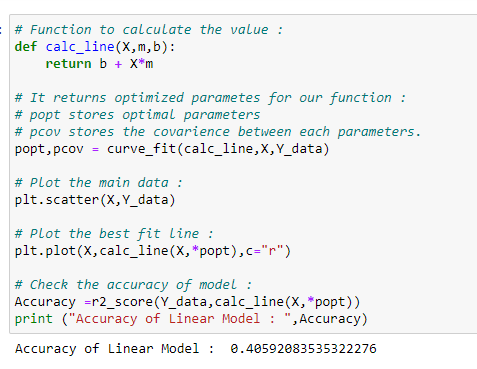
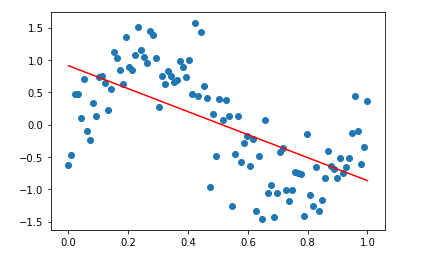
한데 모아보기:
# Import required libraries:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from sklearn.metrics import r2_score
# Generating dataset:
# Y = A*sin(B(X + C)) + D
# A = Amplitude
# Period = 2*pi/B
# Period = Length of One Cycle
# C = Phase Shift (In Radian)
# D = Vertical Shift
X = np.linspace(0,1,100) #(Start,End,Points)
# Here…
# A = 1
# B= 2*pi
# B = 2*pi/Period
# Period = 1
# C = 0
# D = 0
Y = 1*np.sin(2*np.pi*X)
# Adding some Noise :
Noise = 0.4*np.random.normal(size=100)
Y_data = Y + Noiseplt.scatter(X,Y_data,c=”r”)
# Calculate the value:
def calc_sine(x,a,b,c,d):
return a * np.sin(b* ( x + np.radians(c))) + d
# Finding optimal parameters :
popt,pcov = curve_fit(calc_sine,X,Y_data)
# Plot the main data :
plt.scatter(X,Y_data)# Plot the best fit curve :
plt.plot(X,calc_sine(X,*popt),c=”r”)
# Check the accuracy :
Accuracy =r2_score(Y_data,calc_sine(X,*popt))
print (Accuracy)
# Function to calculate the value :
def calc_line(X,m,b):
return b + X*m
# It returns optimized parametes for our function :
# popt stores optimal parameters
# pcov stores the covarience between each parameters.
popt,pcov = curve_fit(calc_line,X,Y_data)
# Plot the main data :
plt.scatter(X,Y_data)# Plot the best fit line :
plt.plot(X,calc_line(X,*popt),c=”r”)
# Check the accuracy of model :
Accuracy =r2_score(Y_data,calc_line(X,*popt))
print (“Accuracy of Linear Model : “,Accuracy)1.6 로그 회귀:
로그 성장의 실 세계 예:
지진의 규모.
소리의 강도.
용액의 산도.
용액의 pH 수준.
화학 반응의 수율.
상품 생산.
유아의 성장.
코로나19 그래프.
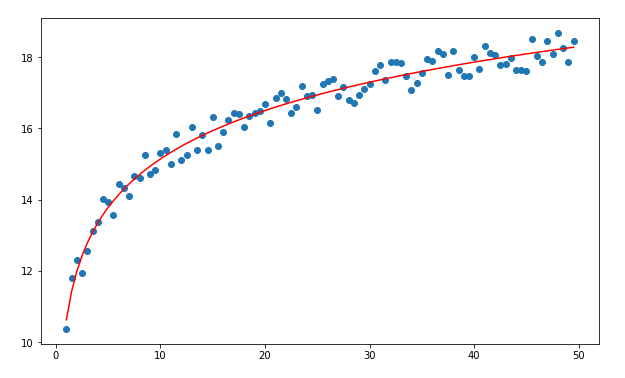
때때로 명제 내에서 기하급수적으로 증가하지만 특정 지점 이후에는 평평해지는 는 데이터가 있습니다. 이러한 경우 로그 회귀를 사용할 수 있습니다.

파이썬 단계별 구현:
a. 필요 라이브러리 임포트:
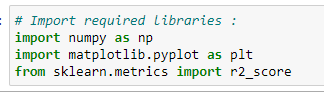
b. 데이터 집합 생성:
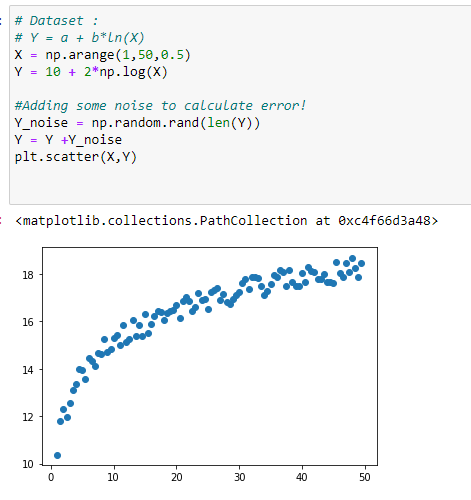
c. 우리의 행렬 X의 첫번째 컬럼:
계수 값들을 찾기 위해서 정규 방정식을 사용 할 것입니다.
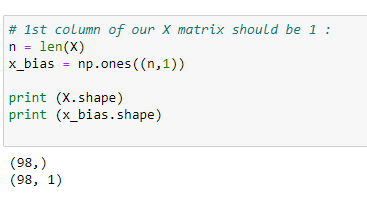
d. Reshaping X:
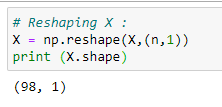
e. 정규 방정식 공식을 이용합니다:
f. 주 행렬 X를 정형화 하기:
g. 전치 행렬 찾기:
h. 행렬 곱셈 수행:
i. 역행렬 찾기:
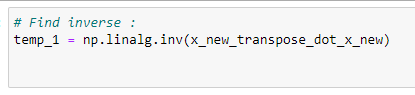
j. 행렬 곱셈:
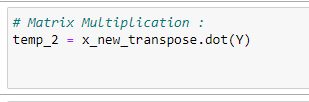
k. 계수 값 찾기:
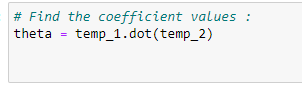
l. 회귀곡선으로 데이터 표시하기:
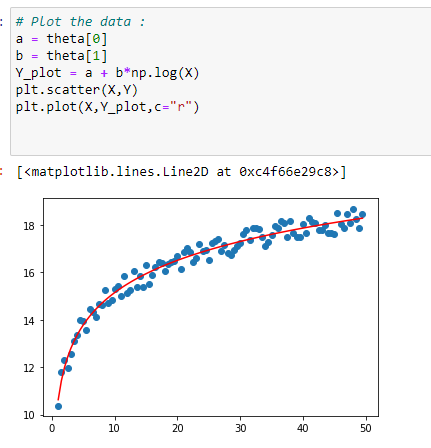
m. 정확도:
한데모아보기
# Import required libraries:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score
# Dataset:
# Y = a + b*ln(X)
X = np.arange(1,50,0.5)
Y = 10 + 2*np.log(X)
#Adding some noise to calculate error!
Y_noise = np.random.rand(len(Y))
Y = Y +Y_noise
plt.scatter(X,Y)
# 1st column of our X matrix should be 1:
n = len(X)
x_bias = np.ones((n,1))
print (X.shape)
print (x_bias.shape)
# Reshaping X :
X = np.reshape(X,(n,1))
print (X.shape)
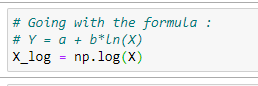
# Going with the formula:
# Y = a + b*ln(X)
X_log = np.log(X)
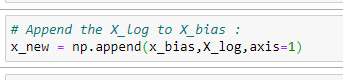
# Append the X_log to X_bias:
x_new = np.append(x_bias,X_log,axis=1)
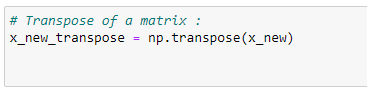
# Transpose of a matrix:
x_new_transpose = np.transpose(x_new)
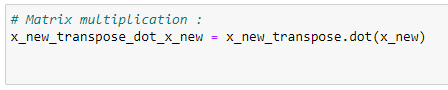
# Matrix multiplication:
x_new_transpose_dot_x_new = x_new_transpose.dot(x_new)
# Find inverse:
temp_1 = np.linalg.inv(x_new_transpose_dot_x_new)
# Matrix Multiplication:
temp_2 = x_new_transpose.dot(Y)
# Find the coefficient values:
theta = temp_1.dot(temp_2)
# Plot the data:
a = theta[0]
b = theta[1]
Y_plot = a + b*np.log(X)
plt.scatter(X,Y)
plt.plot(X,Y_plot,c=”r”)
# Check the accuracy:
Accuracy = r2_score(Y,Y_plot)
print (Accuracy)
면책 조항: 이 기사에 표현된 견해는 저자(들)의 견해이며 Carnegie Mellon University 또는 저자(들)와 관련된 다른 회사(직간접적으로)의 견해를 나타내지 않습니다. 이 글은 최종 제품이 아니라 현재 생각을 반영하고 토론과 개선을 위한 촉매제가 됩니다.
인용
학술적 맥락에서 이 작업을 다음과 같이 인용하십시오.
Shukla, et al., “Machine Learning Algorithms For Beginners with Code Examples in Python”, Towards AI, 2020
BibTex 인용:
@article{pratik_iriondo_chen_2020,
title={Machine Learning Algorithms For Beginners with Code Examples in Python},
url={https://towardsai.net/machine-learning-algorithms},
journal={Towards AI},
publisher={Towards AI Co.},
author={Pratik, Shukla and Iriondo,
Roberto and Chen, Sherwin},
editor={Stanford, StacyEditor},
year={2020},
month={Jun}
}
참고 문서:
[1] Mitchell, Tom. (1997). Machine Learning. McGraw Hill. p. 2. ISBN 0–07–042807–7
[2] Machine Learning, Arthur Samuel, Carnegie Mellon, http://www.contrib.andrew.cmu.edu/~mndarwis/ML.html
[3] Machine Learning (ML) vs. AI, Towards AI, https://towardsai.net/ai-vs-ml
[4] Key Machine Learning Definitions, Towards AI, https://towardsai.net/machine-learning-definitions
Published via Towards AI
추천기사
I. Best Datasets for Machine Learning and Data Science
II. AI Salaries Heading Skyward
III. What is Machine Learning?
IV. Best Masters Programs in Machine Learning (ML) for 2020
V. Best Ph.D. Programs in Machine Learning (ML) for 2020
VI. Best Machine Learning Blogs
VII. Key Machine Learning Definitions
VIII. Breaking Captcha with Machine Learning in 0.05 Seconds
IX. Machine Learning vs. AI and their Important Differences
X. Ensuring Success Starting a Career in Machine Learning (ML)
XI. Machine Learning Algorithms for Beginners
XII. Neural Networks from Scratch with Python Code and Math in Detail
XIII. Building Neural Networks with Python
XIV. Main Types of Neural Networks
XV. Monte Carlo Simulation Tutorial with Python
XVI. Natural Language Processing Tutorial with Python
이상.
'머신러닝' 카테고리의 다른 글
| 파이썬과 머신러닝 (0) | 2024.10.10 |
|---|---|
| 피드포워드 신경망으로 숫자 및 의류 항목 분류 (0) | 2023.04.17 |
| C++에서 데이터 전처리 및 시각화 (1) | 2022.12.09 |
| 선형회귀와 그래프 (0) | 2022.10.12 |
| 선형회귀에 대한 고찰 (2) | 2022.10.07 |