선형회귀는 연속적인 데이터를 평가하기에 좋은 알고리즘으로 알고 있습니다.
물론 식도 알고 있기는 합니다.
문서를 보면, 아 그렇지 하다가도 돌아서면 이제까지 들었던 온갖 용어들에 갇혀버리고 그 속에서 방황하게 되는 군요
소위, 이해 없이 머리만 그떡이는 꼴이라는 것입니다.
예전에 번역 아닌 번역 한 선형 회귀에 대한 문서에 대해서 다시 한 번 얘기를 해보려고 합니다.
선형회귀에 대한 고찰
Linear Regression — ML Glossary documentation Linear Regression is a supervised machine learning algorithm where the predicted output is continuous and has a constant slope. It’s used to predict v..
tobee.tistory.com
데이터를 받아다가 완성을 해 보는 거죠... 그러면 뭔가 남는 게 있지 않을까 하는 맘도 있고
어느 분이 질문하신 내용도 있고 겸사겸사 해보는 것으로 하죠
결과를 먼저 보실려면 동영상을 먼저 보시는 걸로 하시구요
데이터는 카글에서 받아서 쓰는 것으로 합니다.
Advertising.csv
It is data set for linear regrssion
www.kaggle.com
우선 주피터 노트북을 열어다 놓고서, 시작 해 봅니다.
데이터를 읽어 들이는 용도로 판다스를 사용하고,
import pandas as pd그래프를 그리는 용도로 #pyplot 을 사용 하도록 임포트 해 줍니다.
import matplotlib.pyplot as plt여기서, 주피터 노트북 사용에 대해서 알고 싶으시면,
두서없이 적어 놓은 글을 읽어 보셔도 되고 정리 된 다른 사이트를 보셔도 될 듯 하네요..
아나콘다에 케라스 설치하기
#Keras 는 #Python 으로 작성된 고급 신경망 API입니다. 이 딥 러닝 Python 라이브러리는 TensorFl...
blog.naver.com
C/C++, 파이썬 개발환경 설치하기
1. C/C++ 개발 환경 설치하기 너무도 많이 언급해서 이제는 약간 지겨워 지려고 하는 GCC 개발 환경에...
blog.naver.com
위에 꺼 어떻게든 설치하시면, 다음 배치 스크립트가 필요 할 수도 있죠.
SET ANACONDA_HOME=C:\DEV\SDK\Anaconda3
SET ANCONDA_VARS=%ANACONDA_HOME%;%ANACONDA_HOME%\Scripts;%ANACONDA_HOME%\Lib;%ANACONDA_HOME%\DLLs;
SET PATH=.;%ANCONDA_VARS%;%ANACONDA_HOME%\BIN;%ANACONDA_HOME%\condabin;%ANACONDA_HOME%\Library\bin;%PATH%;.
echo call cmd /K "activate base"
call cmd /K "jupyter notebook"데이터를 한번 열어 봅니다.
df = pd.read_csv('./Advertising.csv')
dfUnnamed: 0 은 별로 필요가 없어 보이네요.
그리고 뭐 Company는 없고 TV나 Newspaper 도 보이네요
그냥 확~ 지우죠 뭐 ㅋㅋ
dset = df.copy()
dset = dset.drop('Unnamed: 0', axis = 1)
dset = dset.drop('Radio', axis = 1)
dset = dset.drop('Newspaper', axis = 1)
dset

아시다 시피 우리는 예상 매출을 이렇게 잡았죠

다음 비용함수를 가지고서
def cost_function(radio, sales, weight, bias):
companies = len(radio)
total_error = 0.0
for i in range(companies):
total_error += (sales[i] - (weight*radio[i] + bias))**2
return total_error / companies경사하강법을 사용 하여 위의 수식에서 비용이 최소가 되는 값들을 찾아 나가야 한다고 ...그렇게 쓰여 있습니다.
다음과 같이 weight, bias 값을 업데이트 합니다.
번역본에 쓰여진 편미분으로 만들어 진 식으로 계속 업데이트가 진행 되고 있군요.

def update_weights(radio, sales, weight, bias, learning_rate):
weight_deriv = 0
bias_deriv = 0
companies = len(radio)
for i in range(companies):
# Calculate partial derivatives
# -2x(y - (mx + b))
weight_deriv += -2*radio[i] * (sales[i] - (weight*radio[i] + bias))
# -2(y - (mx + b))
bias_deriv += -2*(sales[i] - (weight*radio[i] + bias))
# We subtract because the derivatives point in direction of steepest ascent
weight -= (weight_deriv / companies) * learning_rate
bias -= (bias_deriv / companies) * learning_rate
return weight, bias다 그럼 기본 함수들을 다 만들었으니, 모델을 훈련 하는 함수가 있습니다.
여기서 learning_rate 는 얼만큼 빨리 혹은 느리게 계산을 해 나갈 것이냐 라는 느낌으로 알고 있습니다.
( 심각하게 물으시면 몰라요~~)
그러면, 훈련 함수가 남았네요.
여기서 한 가지 이 값들로 인해서 우리의 예측 선이 어떻게 예쁘게(?) 변했는 지를 알기 위해서는 그래프를 그려봐야 할 것 같은 데요
그렇게 하기 위해서는 값들을 몇 개 저장 해야 할 것 같습니다.
def train(radio, sales, weight, bias, learning_rate, iters):
cost_history = []
weights = []
biass = []
each_iter = []
for i in range(iters):
weight,bias = update_weights(radio, sales, weight, bias, learning_rate)
#Calculate cost for auditing purposes
cost = cost_function(radio, sales, weight, bias)
cost_history.append(cost)
each_iter.append(i)
# Log Progress
if i % 10 == 0:
# print "iter={:d} weight={:.2f} bias={:.4f} cost={:.2}".format(i, weight, bias, cost)
print ('iter={:d} weight={:.2f} bias={:.4f} cost={:.2}'.format(i, weight, bias, cost))
biass.append(bias)
weights.append(weight)
#predict_sales(radio, weight, bias)
return weight, bias, cost_history, biass, weights, each_iter새로운 리스트가 세개 인데요,
weights = [], 각 각 계산 된 weight 값들
biass = [], 각 각 계산 된 bias 값들
each_iter = [] 마지막으로 비용이 어떻게 줄었는가를 알기 위해서 각 반복 단계의 인덱스를
저장 하겠습니다.
그리고 초기 값을 다음과 같이 정했습니다. 여기서 learning_rate 는 사실 제 맘대로 정했습니다.
일반적으로 그렇게 크지 않은 값을 생각 하면서 정했어요...
weight=.03
bias=.0014
iters=60
learning_rate=.00089그리고 값을 배열로 뽑아다가 저장해 놓고, 한 번 뿌려 봅시다
radio=dset['Radio'].values
sales=dset['Sales'].values
plt.scatter(radio, sales, alpha=0.5)
plt.xlabel("Radio")
plt.ylabel("Sales")
plt.title("Linear REGRESSION")
plt.show()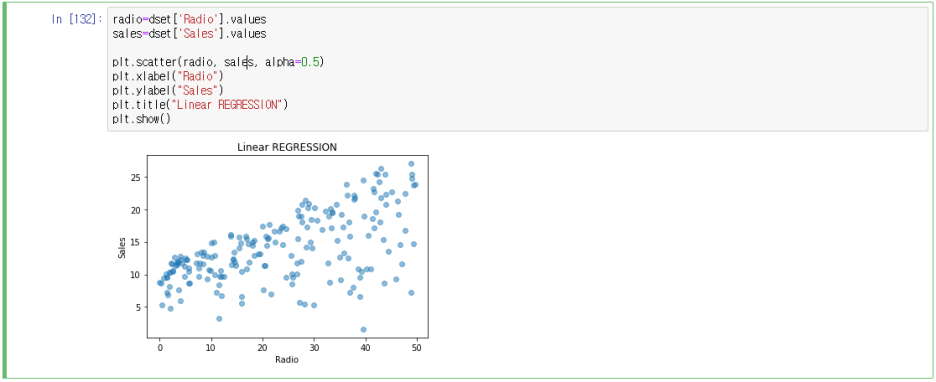
역시, 주피터 노트북... 이군요
훈련을 진행하구요
weight, bias, cost_history, biass, weights, each_iter = train(radio, sales, weight, bias, learning_rate, iters)
진행해 보니 30 부터는 비용이 줄어 들지 않는 것을 확인 할 수가 있습니다
최종적으로 저장 된 값의 그래프를 한 번 보도록 하겠습니다.
plt.scatter(radio, sales, alpha=0.5)
X1=predict_sales(radio, weight, bias)
#plt.plot(radio, X1, color="r", linestyle="dashed")
plt.plot(radio, X1, color="r", linewidth=1)
plt.xlabel("Radio")
plt.ylabel("Sales")
plt.title("Linear REGRESSION")
plt.show()
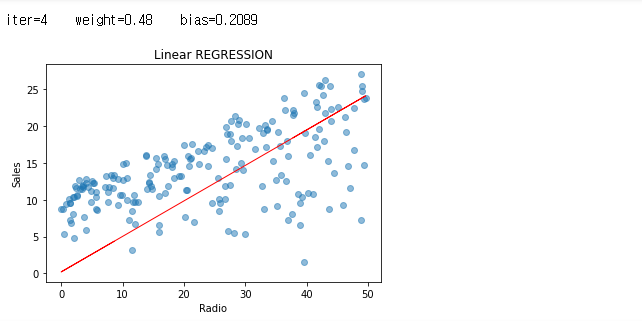
예쁘게 보이는 것 같은데요??
그래도, 반복 중에 일어났던 값들에 대해서도 한 번 그래프를 보도록 하겠습니다.
iters = len(weights)
for i in range(iters):
plt.scatter(radio, sales, alpha=0.5)
weight = weights[i]
bias = biass[i]
print ('iter={:d} weight={:.2f} bias={:.4f}'.format(i, weight, bias))
X1=predict_sales(radio, weight, bias)
plt.plot(radio, X1, color="r", linewidth=1)
plt.xlabel("Radio")
plt.ylabel("Sales")
plt.title("Linear REGRESSION")
plt.show()





자, 그래서 우리의 비용은 어디에서 급격하게 줄었으며, 그 이후로 거의 변화가 없었는 지 여부를 확인 해 볼 차례 입니다.
from matplotlib import rc
import matplotlib.font_manager as fm
font_path = 'C:\\WINDOWS\\Fonts\\NGULIM.TTF'
font = fm.FontProperties(fname=font_path).get_name()
rc('font', family=font)
plt.plot(cost_history, each_iter, color="r", linewidth=1)
plt.xlabel("Cost(비용)")
plt.ylabel("Training Iterations")
plt.title("Linear REGRESSION2")
plt.show()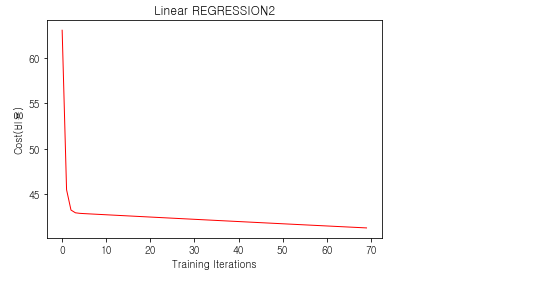
여하튼 뭔가 계속 조금씩 내려가는 느낌이네요...ㅋㅋㅋ
맘에 안드는 그래프가 나온 것 같은 데요 그건 나중에 다시 한 번 조정 해 보는 것으로 하겠습니다.
Tip. 그래프 글자깨짐
파이썬 그래프 상에서 폰트가 깨지면 다음과 같이 font 리스트를 한 번 출력해 보고 무난한 것을 골라보면 됩니다.
위에서는 무난한 굴림을 사용 했습니다.
font_list = fm.findSystemFonts(fontpaths = None, fontext = 'ttf')
font_cnt = len(font_list[:])
for i in range(font_cnt) :
print(font_list[i])'머신러닝' 카테고리의 다른 글
| 피드포워드 신경망으로 숫자 및 의류 항목 분류 (0) | 2023.04.17 |
|---|---|
| 파이썬 코드 예제 - 초보자를 위한 머신러닝 알고리즘 (1) | 2023.04.05 |
| C++에서 데이터 전처리 및 시각화 (1) | 2022.12.09 |
| 선형회귀에 대한 고찰 (3) | 2022.10.07 |
| 기계 학습 시각화에 대한 간단한 가이드 (0) | 2022.04.27 |

