- 소개
- 단순 회귀
- 예측 결정
- 비용 함수
- 경사하강
- 훈련
- 모델 평가
- 요약
- 다중변수 회귀
- 복잡도 증가
- 정규화
- 예측 결정
- 가중치 조기화
- 비용함수
- 경사하강
- 행렬 단순화하기
- 바이어스 항
- 모델 평가
소개
선형 회귀는 예측 된 출력이 연속적이고 일정한 기울기를 갖는 지도 머신 러닝 알고리즘입니다.
값을 카테고리 (예 : 고양이, 개)로 분류하지 않고 연속 범위 (예 : 판매, 가격) 내에서 값을 예측하는 데 사용됩니다.
두 가지 주요 유형이 있습니다:
단순 회귀
단순 선형 회귀는 전통적인 기울기-절편 형태를 사용합니다. 여기서 m과 b는 알고리즘이 가장 정확한 예측을 얻기 위해 “학습”하려고하는 변수입니다.
x는 입력 데이터를 나타내고 y는 예측을 나타냅니다.
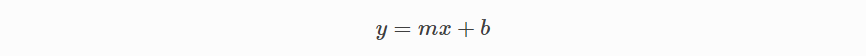
다중변수(Multivariable) 회귀
보다 복잡한 다중 변수 선형 방정식은 다음과 같이 보일 수 있습니다. 여기서 w는 계수 또는 가중치를 나타내며 모델이 학습 될 것입니다.
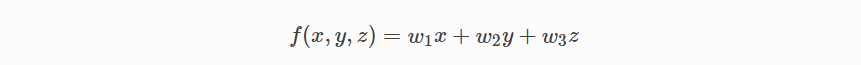
변수 x, y, z는 각 관측치에 대한 속성 또는 고유 한 정보를 나타냅니다.
판매 예측의 경우 이러한 속성으로 라디오, TV 및 신문에 내는 회사의 광고비가 포함될 수 있습니다.
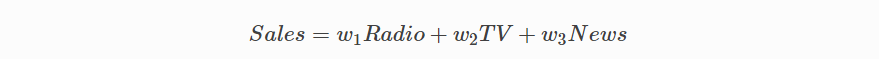
단순 회귀
회사가 매년 라디오 광고에 소비하는 금액과 연간 판매량을 기준으로 연간 판매량에 대한 데이터 군을 제공한다고 가정 해 봅시다.
우리는 회사가 라디오 광고에 소비하는 금액에 따라 판매 단위를 예측할 수있는 방정식을 개발하려고 노력하고 있습니다. 행 (관측)은 회사를 나타냅니다.
|
Company
|
Radio ($)
|
Sales
|
|
Amazon
|
37.8
|
22.1
|
|
Google
|
39.3
|
10.4
|
|
Facebook
|
45.9
|
18.3
|
|
Apple
|
41.3
|
18.5
|
예측 결정
우리의 예측 함수는 회사의 라디오 광고 지출과 현재 가중치 및 바이어스 값을 고려한 예상 매출을 출력합니다.
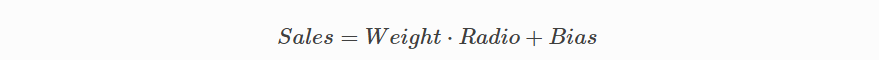
가중치(Weight)
라디오 독립 변수의 계수. 기계 학습에서는 계수 가중치(coefficients weights)라고합니다.
라디오(Radio)
독립 변수. 기계 학습에서 우리는 이 값을 variables feature 라고 합니다.
바이어스(Bias)
y 축을 지나는 선의 절편. 기계 학습에서는 인터셉트 바이어스라고 합니다.
바이어스는 우리가 만드는 모든 예측들의 오프셑 입니다.
우리의 알고리즘은 가중치와 바이어스에 대한 올바른 값들을 학습하려고 할 것입니다. 이 훈련이 끝날 즈음, 우리의 방정식은 가장 알맞은 선에 가까워 질 것입니다.
코드
def predict_sales(radio, weight, bias):
return weight*radio + bias비용함수
예측 함수가 멋져 보이겠지만, 우리의 목적은 정말 예측을 위한 것이 아닙니다. 우리가 필요한 것은 비용 함수이므로 우리는 이 가중치들의 최적화 부터 진행 할 수 있습니다.
그럼 MSE (L2)를 우리의 비용함수로 사용 해 봅시다. MSE는 관측치의 실제 값과 예측 된 값의 평균 제곱 차이를 측정합니다.
결과는 현재 가중치 집합과 관련된 비용 또는 점수를 나타내는 단일 숫자입니다.
우리의 목표는 모델의 정확성을 향상시키기 위해서 이 MSE 값을 최소화하는 것입니다.
수학식
간단한 선형 방정식 y = mx + b가 주어지면 MSE의 계산은 다음과 같습니다.
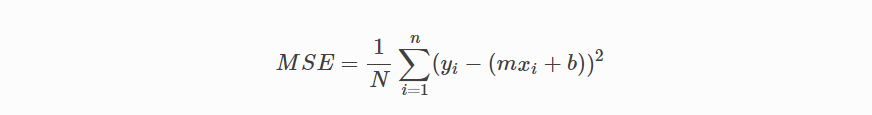
주의
- N: 총 관측치 수 (데이터 포인트) 입니다.
- yi는 관측치의 실제 값이고 mxi + b는 우리의 예측입니다
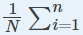
는 평균입니다.
코드
def cost_function(radio, sales, weight, bias):
companies = len(radio)
total_error = 0.0
for i in range(companies):
total_error += (sales[i] - (weight*radio[i] + bias))**2
return total_error / companies경사하강
MSE 값을 최소화하기 위해 경사하강(Gradient Descent)을 사용하여 비용 함수의 기울기를 계산합니다.
경사하강은 기울기(현재 가중치를 사용하는 비용 함수의 기울기)를 찾기위해 현재 비용 함수의 미분을 사용하여 계산 된 가중치의 오류를 확인하고 기울기의 반대 방향으로 이동하도록 가중치를 변경하는 것으로 구성됩니다. 기울기가 기울기가 아래쪽이 아닌 위쪽을 가리킨다면 기울기의 반대 방향으로 이동해야 하므로 오류를 줄이기 위해 반대 방향으로 움직여야 합니다.
수학 식
우리가 제어 할 수있는 비용 함수의 두 가지 매개 변수 (계수)가 존재합니다 : 가중치 m과 바이어스 b.
최종 예측에 미치는 영향을 고려해야하기 때문에 편미분을 사용합니다.
편미분을 찾기 위해 연쇄 규칙(Chain rule)을 사용합니다. (y- (mx + b))^ 2는 실제로 2 개의 중첩 함수 인 내부 함수 y- (mx + b)와 외부 함수 x^2이므로 연쇄 규칙이 필요합니다.
비용 함수로 돌아 가서 :
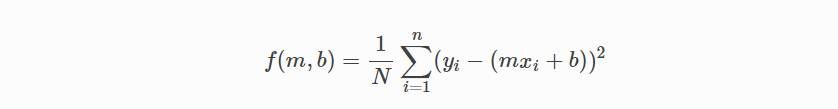
다음 수식을 사용하여:
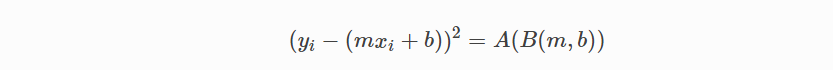
미분 식을 다음과 같이 두개로 나눌 수 있고
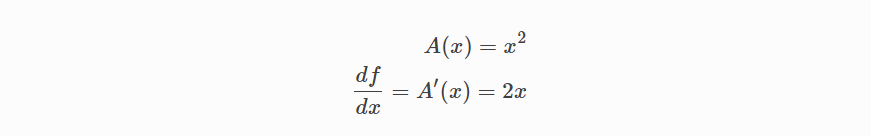
그런 다음
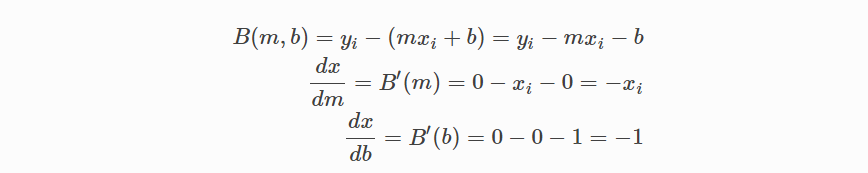
그리고 다음 식으로 연쇄규칙 사용하여 표현 하며:
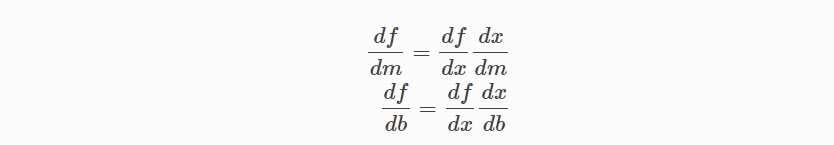
다음의 미분 방정식을 얻기 위한 각 부분을 끼워 넣습니다.
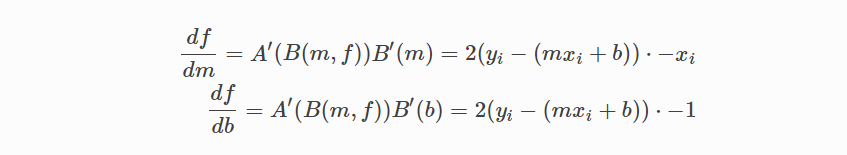
이 비용 함수의 기울기를 다음과 같이 계산할 수 있습니다.

코드
그래디언트를 해결하기 위해 새로운 가중치 및 바이어스 값을 사용하여 우리의 데이터 포인트에 대한 반복 통해서 편 미분의 평균을 취합니다.결과 기울기는 현재 위치에서 비용 함수의 기울기(예 : 가중치 및 바이어스)와 비용 함수를 줄이기 위해 업데이트해야하는 방향을 알려 줍니다. (그라디언트 반대 방향으로 이동)
업데이트의 크기는 학습 률에 의해 제어됩니다.
def update_weights(radio, sales, weight, bias, learning_rate):
weight_deriv = 0
bias_deriv = 0
companies = len(radio)
for i in range(companies):
# Calculate partial derivatives
# -2x(y - (mx + b))
weight_deriv += -2*radio[i] * (sales[i] - (weight*radio[i] + bias))
# -2(y - (mx + b))
bias_deriv += -2*(sales[i] - (weight*radio[i] + bias))
# We subtract because the derivatives point in direction of steepest ascent
weight -= (weight_deriv / companies) * learning_rate
bias -= (bias_deriv / companies) * learning_rate
return weight, bias
훈련
모델 훈련은 여러 번 데이터 세트의 반복을 통해서 예측 방정식을 반복적으로 개선하는 프로세스이며,
비용함수(그라디언트)의 기울기가 가리키는 방향 내으로 각 반복에서 가중치와 바이어스 값을 업데이트 하게 됩니다.
훈련은 허용가능한 오차 임계치에 도달하거나, 후속 훈련 반복으로 인해 비용이 절감되지 않으면 완료됩니다.
학습하기 전에 가중치를 초기화하고 (기본값 설정) 하이퍼 파라미터를 설정하고 (학습 속도 및 반복 횟수) 각 반복에 대한 진행 상황을 기록 할 준비를해야합니다.
코드
def train(radio, sales, weight, bias, learning_rate, iters):
cost_history = []
for i in range(iters):
weight,bias = update_weights(radio, sales, weight, bias, learning_rate)
#Calculate cost for auditing purposes
cost = cost_function(radio, sales, weight, bias)
cost_history.append(cost)
# Log Progress
if i % 10 == 0:
print "iter={:d} weight={:.2f} bias={:.4f} cost={:.2}".format(i, weight, bias, cost)
return weight, bias, cost_history모델 평가
모델이 동작하면 반복 할 때마다 비용이 감소합니다.
로깅
iter=1 weight=.03 bias=.0014 cost=197.25
iter=10 weight=.28 bias=.0116 cost=74.65
iter=20 weight=.39 bias=.0177 cost=49.48
iter=30 weight=.44 bias=.0219 cost=44.31
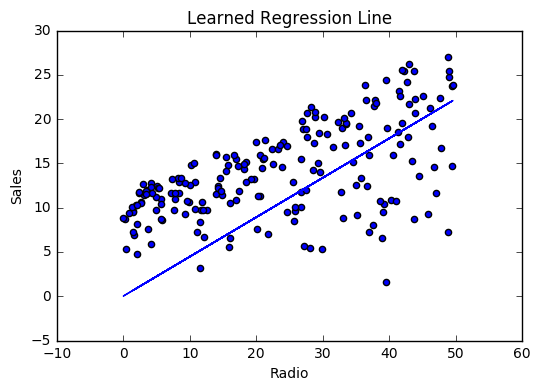
iter=30 weight=.46 bias=.0249 cost=43.28시각화
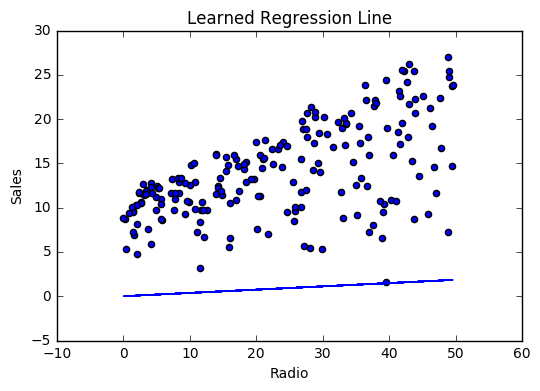
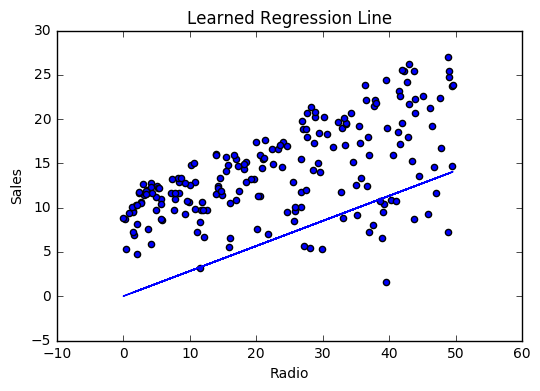
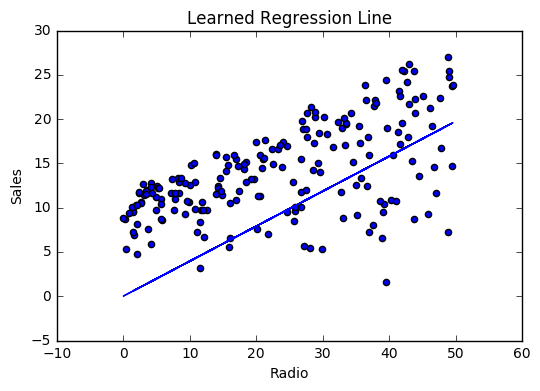
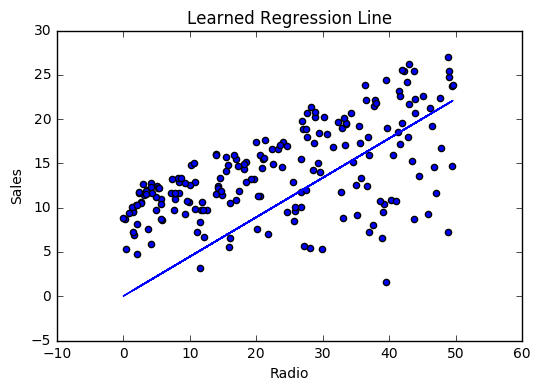
비용 이력
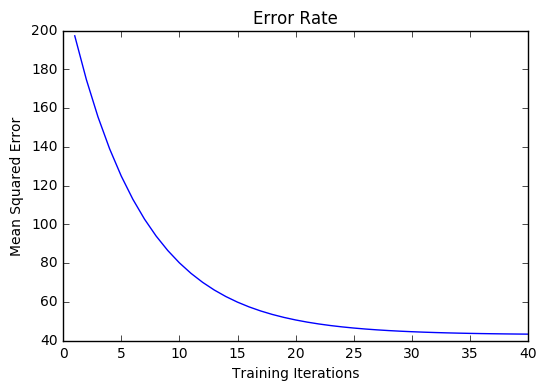
요약
최상의 값인 가중치 (.46) 및 바이어스 (.25)에 대해서 학습함으로써 이제 radio 광고 투자를 기반으로 향후 판매를 예측하는 방정식을 갖게되었습니다.
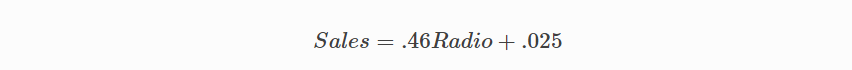
다중변수 회귀
회사 목록에 대한 TV, 라디오 및 신문 광고 지출에 대한 데이터가 제공되고 판매 목표로 매출을 예측하는 것이 목표라고 가정 해 보겠습니다.
|
Company
|
TV
|
Radio
|
News
|
Units
|
|
Amazon
|
230.1
|
37.8
|
69.1
|
22.1
|
|
Google
|
44.5
|
39.3
|
23.1
|
10.4
|
|
Facebook
|
17.2
|
45.9
|
34.7
|
18.3
|
|
Apple
|
151.5
|
41.3
|
13.2
|
18.5
|
복잡도 증가
feature의 수가 증가함에 따라 모델의 복잡성이 증가하고 데이터를 시각화하거나 이해하기가 점점 어려워집니다.
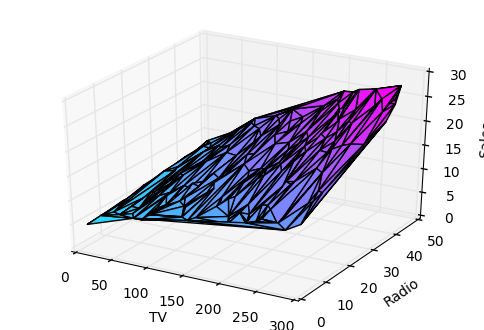
한 가지 해결책은 데이터를 분리하고 한 번에 1-2 개의 피처를 비교하는 것입니다. 이번 예에서는 라디오 및 TV 투자가 판매에 미치는 영향을 살펴 봅니다.
정규화
피처의 수가 증가함에 따라 그라디언트를 계산하는 데 시간이 오래 걸립니다.
모든 값이 동일한 범위 내에 있도록 입력 데이터를 "정규화"하여이 속도를 높일 수 있습니다.
이는 표준 편차가 높거나 속성 범위가 다른 데이터 군에서 특히나 중요합니다.
우리의 목표는 지금 우리의 피처들을 정규화하여 모든 범위가 -1에서 1이되도록하는 것입니다.
코드
For each feature column {
#1 Subtract the mean of the column (mean normalization)
#2 Divide by the range of the column (feature scaling)
}우리의 입력은 TV, 라디오 및 신문 데이터를 포함하는 200 x 3 행렬입니다. 우리의 출력은 -1과 1 사이의 모든 값을 가진 같은 모양의 정규화 된 행렬입니다.
def normalize(features):
**
features - (200, 3)
features.T - (3, 200)
We transpose the input matrix, swapping
cols and rows to make vector math easier
**
for feature in features.T:
fmean = np.mean(feature)
frange = np.amax(feature) - np.amin(feature)
#Vector Subtraction
feature -= fmean
#Vector Division
feature /= frange
return features주의
행렬 수학.
계속하기 전에 기본 선형 대수 개념과 numpy.dot ()와 같은 numpy 함수를 이해하는 것이 중요합니다.
예측 결정
예측 함수는 현재 가중치 (계수)와 회사의 TV, 라디오 및 신문 지출을 고려한 예상 매출을 출력합니다. 우리 모델은 비용 함수를 가장 줄이는 가중치를 찾기 위해서 노력할 것입니다.
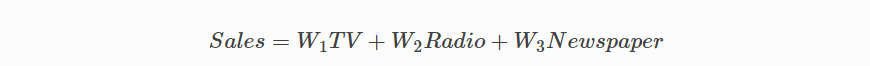
def predict(features, weights):
**
features - (200, 3)
weights - (3, 1)
predictions - (200,1)
**
predictions = np.dot(features, weights)
return predictions가중치 초기화
W1 = 0.0
W2 = 0.0
W3 = 0.0
weights = np.array([
[W1],
[W2],
[W3]
])비용함수
이제 모델의 성능을 검사하기위해 비용 함수가 필요합니다.
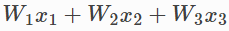
으로 교체한다는 점을 제외하면 계산은 동일합니다.
또한 미분 계산을 더 간단하게하기 위해 표현식을 2로 나눕니다.
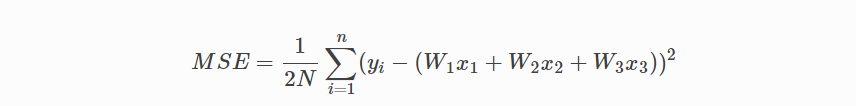
def cost_function(features, targets, weights):
**
features:(200,3)
targets: (200,1)
weights:(3,1)
returns average squared error among predictions
**
N = len(targets)
predictions = predict(features, weights)
# Matrix math lets use do this without looping
sq_error = (predictions - targets)**2
# Return average squared error among predictions
return 1.0/(2*N) * sq_error.sum()
def update_weights(features, targets, weights, lr):
'''
Features:(200, 3)
Targets: (200, 1)
Weights:(3, 1)
'''
predictions = predict(features, weights)
#Extract our features
x1 = features[:,0]
x2 = features[:,1]
x3 = features[:,2]
# Use matrix cross product (*) to simultaneously
# calculate the derivative for each weight
d_w1 = -x1*(targets - predictions)
d_w2 = -x2*(targets - predictions)
d_w3 = -x3*(targets - predictions)
# Multiply the mean derivative by the learning rate
# and subtract from our weights (remember gradient points in direction of steepest ASCENT)
weights[0][0] -= (lr * np.mean(d_w1))
weights[1][0] -= (lr * np.mean(d_w2))
weights[2][0] -= (lr * np.mean(d_w3))
return weights여기까지가 다중변수 회귀의 모든 것 입니다.
행렬로 단순화하기
위의 경사하강 코드에는 중복이 많습니다. 어떻게 개선 할 수 있을까요?
리팩토링하는 한 가지 방법은 우리의 피처과 가중치를 반복하게 하도록 함수가 여러 피처를 처리하도록 하는 것입니다.
하지만 vectorized gradient descent이라는 또 다른 더 좋은 기술이 존재하고 있습니다.
수학식
위와 동일한 공식을 사용하지만 한 번에 하나의 기능을 사용하는 대신 모든 피처과 가중치를 동시에 처리하기 위해 행렬 곱셈을 사용합니다. xi 항을 단일 피처 행렬 X로 바꿉니다.
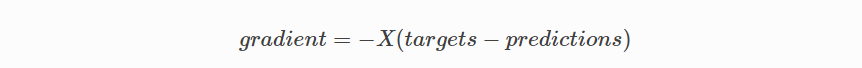
코드
X = [
[x1, x2, x3]
[x1, x2, x3]
.
.
.
[x1, x2, x3]
]
targets = [
[1],
[2],
[3]
]
def update_weights_vectorized(X, targets, weights, lr):
**
gradient = X.T * (predictions - targets) / N
X: (200, 3)
Targets: (200, 1)
Weights: (3, 1)
**
companies = len(X)
#1 - Get Predictions
predictions = predict(X, weights)
#2 - Calculate error/loss
error = targets - predictions
#3 Transpose features from (200, 3) to (3, 200)
# So we can multiply w the (200,1) error matrix.
# Returns a (3,1) matrix holding 3 partial derivatives --
# one for each feature -- representing the aggregate
# slope of the cost function across all observations
gradient = np.dot(-X.T, error)
#4 Take the average error derivative for each feature
gradient /= companies
#5 - Multiply the gradient by our learning rate
gradient *= lr
#6 - Subtract from our weights to minimize cost
weights -= gradient
return weights
바이어스 항
우리의 훈련 함수는 간단한 선형 회귀와 동일하지만, 실행하기 전에 마지막으로 한 가지를 조정할 것입니다.
: 바이어스 항을 우리의 피처 행렬에 추가 하는 것 입니다.
이번 예에서 회사가 광고를 중단한다고 매출이 0이 될 가능성은 거의 없습니다. 그 이유는 과거 광고, 기존 고객 관계, 소매점 및 영업 사원등이 이유가 될 수 있겠죠.
바이어스 항은 base case를 포착하는 데 도움을 줍니다.
base case : 순환되지 않고 종료 되는 case
코드
아래에서 피처 행렬에 상수 1을 추가합니다. 이 값을 1로 설정하면 바이어스 항이 상수로 바뀝니다.
bias = np.ones(shape=(len(features),1))
features = np.append(bias, features, axis=1)모델 평가
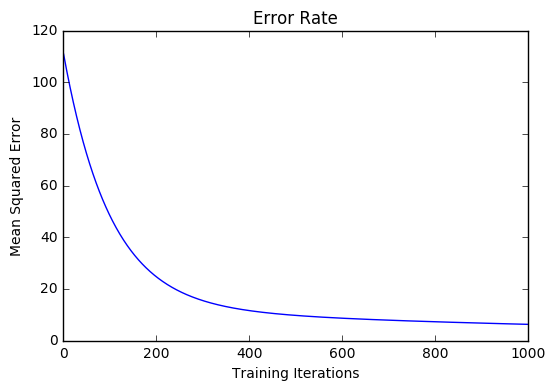
학습 속도가 .0005 인 1000 회 반복을 통해 모델을 학습 한 후 마침내 예측에 사용할 수있는 가중치 군에 도달합니다.
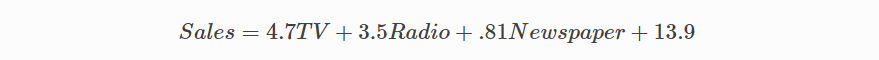
MSE 비용이 110.86에서 6.25로 감소했습니다.
참고
[1] https://en.wikipedia.org/wiki/Linear_regression
[2] http://www.holehouse.org/mlclass/04_Linear_Regression_with_multiple_variables.html
[3] http://machinelearningmastery.com/simple-linear-regression-tutorial-for-machine-learning
[4] http://people.duke.edu/~rnau/regintro.htm
[5] https://spin.atomicobject.com/2014/06/24/gradient-descent-linear-regression
[6] https://www.analyticsvidhya.com/blog/2015/08/common-machine-learning-algorithms
'머신러닝' 카테고리의 다른 글
| 피드포워드 신경망으로 숫자 및 의류 항목 분류 (0) | 2023.04.17 |
|---|---|
| 파이썬 코드 예제 - 초보자를 위한 머신러닝 알고리즘 (1) | 2023.04.05 |
| C++에서 데이터 전처리 및 시각화 (1) | 2022.12.09 |
| 선형회귀와 그래프 (0) | 2022.10.12 |
| 기계 학습 시각화에 대한 간단한 가이드 (0) | 2022.04.27 |
